题目描述

一维差分+一维前缀和+排序不等式

样例

import java.util.*;

/*
    前缀和，差分，排序不等式

    前缀和：用来算区间[l,r]的和

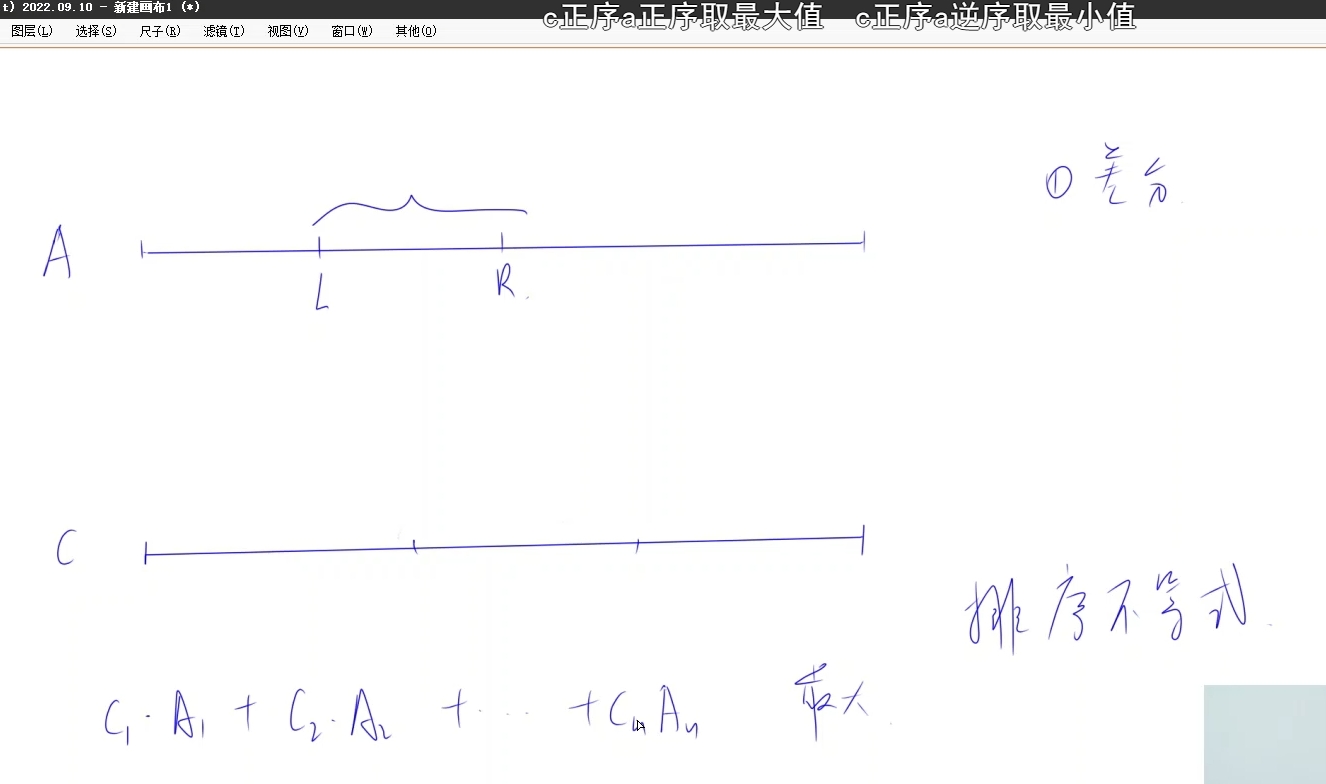
    差分：是用来统计区间[l,r]出现的次数   用差分统计就快得多

    排序不等式：C正序A正序取最大值，C正序A逆序取最小值  公式： C1*A1 + C2*A2 +...+ Cn*An  
    就是出现频率最大对应最大的数，取最大值； 出现频率最大对应最小的数，取最小值
    公式刚好可以算出来本题的调整后各次区间的求和的总值。
    各次区间的求和的总值其实就是该数*出现的次数的总值
*/

public class Main {
    static final int N = 100010;
    static int[] a = new int[N], cnt = new int[N];
    static long[] s = new long[N];
    public static void insert(int l, int r) {
        cnt[l] += 1;
        cnt[r + 1] -= 1;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for (int i = 1; i <= n; i ++) {
            a[i] = sc.nextInt();
            s[i] = s[i - 1] + a[i];
        }

        long sum = 0;
        int m = sc.nextInt();
        while (m -- > 0) {
            int l = sc.nextInt(), r = sc.nextInt();
            //计算初始的前缀和
            sum += s[r] - s[l - 1];
            //计算出现频率的差分数组
            insert(l, r);
        }

        //还原出现频率的数组
        for (int i = 1; i <= n; i ++) cnt[i] += cnt[i - 1];

        //对数组a的下标从fromIndex到toIndex-1的元素排序，注意：下标为toIndex的元素不参与排序哦！
        //对于出现频率和数字，都用正序。
        Arrays.sort(cnt, 1, n + 1); Arrays.sort(a, 1, n + 1);
        //可能爆int
        long res = 0;
        //利用排序不等式
        for (int i = 1; i <= n; i ++) res += (long) a[i] * cnt[i];
        System.out.println(res - sum);
    }
}

————————————————————————————————————————————————————————————————————————————————