AcWing 282. 石子合并

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 282. 石子合并原题链接简单

作者：

TaoZex , 2019-05-29 12:21:25 , 所有人可见 , 阅读 9536

43

20

更新：图源自算法基础课程讲解
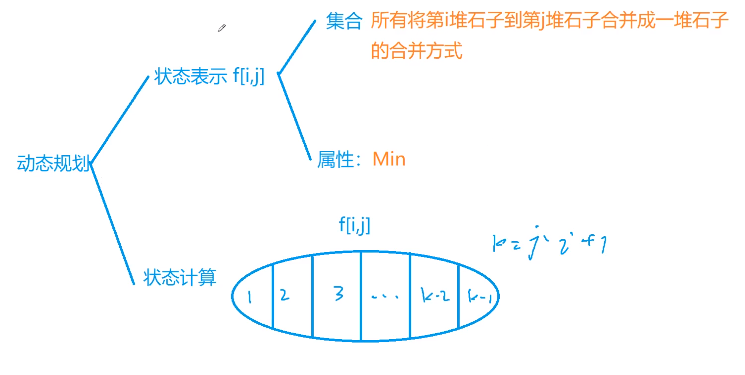
捕获2.PNG

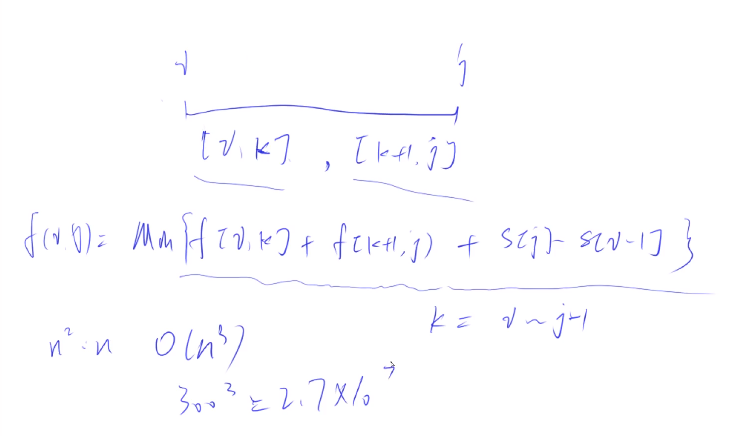
捕获1.PNG
具有明显的阶段性（相邻的合并），所以只能区间dp，不能贪心

#include<bits/stdc++.h>
using namespace std;

const int N=310,INF=0x3f3f3f3f;
int f[N][N];
int s[N];
int n;

int main(){
    cin>>n;
    memset(f,INF,sizeof(f));     //记得初始化
    for(int i=1;i<=n;i++){
         cin>>s[i];
         f[i][i]=0;             //初始化
    }
    for(int i=1;i<=n;i++) s[i]+=s[i-1];

    for(int len=2;len<=n;len++){
        for(int l=1;l+len-1<=n;l++){
            int r=l+len-1;
            for(int k=l;k<r;k++){
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
            }    
        }
    }
    cout<<f[1][n]<<endl;
    return 0;
}

另一种区间划分方式：

#include<bits/stdc++.h>
using namespace std;

const int N=310;
int f[N][N],a[N],s[N];
int n;


int main(){
    cin>>n;
    memset(f,0x3f,sizeof(f));
    for(int i=1;i<=n;i++){
         cin>>a[i];
         s[i]=s[i-1]+a[i];
         f[i][i]=0;
    }

    for(int len=2;len<=n;len++){
        for(int l=1;l+len-1<=n;l++){
            int r=l+len-1;
            for(int k=l+1;k<=r;k++){
                f[l][r]=min(f[l][r],f[l][k-1]+f[k][r]+s[r]-s[l-1]);
            }
        }
    }

    cout<<f[1][n]<<endl;
}

77 评论

大树101 2021-08-03 16:07

y总说的最后一步我没明白s[j]-s[i-1]

大树101 2021-08-03 16:08

为什么最后一步是这个

TaoZex 2021-08-03 18:39 回复了大树101 的评论

s代表前缀和数组，s[j]-s[i-1]代表a[i]到a[j]的和

大树101 2021-08-03 18:54 回复了 TaoZex 的评论

就是不理解两俩合并之后权重改变了为什么还可以用原来的前缀和来更新

TaoZex 2021-08-03 19:34 回复了大树101 的评论

左边的区间[l,k-1]和右边的区间[k,r]合并，此时左边的区间和为s[k-1]-s[l-1],右边的区间和为s[r]-s[k-1],状态转移时这两个区间和要相加，即s[j]-s[i-1]

大树101 2021-08-04 14:14 回复了 TaoZex 的评论

噢噢明白了谢谢

TaoZex 2021-08-04 14:15 回复了大树101 的评论

客气

KenChow 2021-11-22 21:58 回复了 TaoZex 的评论

Thanks♪(･ω･)ﾉ

aiyu 2022-08-13 21:12

我认为有个更好的理解方式，[l,k] [k + 1,r] 分别代表两个区间，那么之前这两个区间产生的代价是f[l][k-1]+f[k][r]，现在我想要合并，就是计算[l, r]的和，两者加起来就是更新

Zzint 2022-10-26 19:53 回复了 aiyu 的评论

我补充个例子有两堆石子，第一堆个数为3，第二堆个数为2 而合并代价是3+2+（3+2）

Deteriorate 2023-03-12 19:01

假设有4堆石子:1 3 5 2
i=1,k=2,j=4
f[1,2]:将第一堆和第二堆这两堆石子合并成一堆石子
f[3,4]:将第三堆和第四堆这两堆石子合并成一堆石子
所以经过f[1,2]+f[3,4]后我们就成功将1 3 5 2这四堆石子合并成了4 7 这两堆石子
不过别忘了题目要求的是将这四堆石子合并成一堆石子
所以我们还需将4 7 这两堆石子合并成一堆石子
因此还需付出4+7=11的代价；而11=[1,4]的前缀和
总代价:(1+3)+(5+2)+4+7=22