$\Huge\color{orchid}{点击此处获取更多干货}$

生成树，最小生成树

无向图的生成树指的是这个图的极小连通子图，它的节点数和原图的节点数相同，但是边数比节点数还少1，这是能够构成连通图的最少边数，这样构成的图结构就相当于树结构了。
生成树可以有不止一种，其边权总和也不完全相同，这些生成树中边权总和最小的就是最小生成树（Mininum Spanning Tree)，最小生成树的结构也不唯一，但是构成最小生成树的边权总和是唯一的。
最小生成树算法主要有两种：Prim算法和Kruskal算法（考研都有可能考），这里主要介绍Prim算法

Prim算法

Prim算法过程中将所有节点分为两类，一类是已经加入MST的节点（$S$类），另一类是未加入MST的节点（$E$类），算法流程如下：
0. 选定一个节点视作$S$类，其余节点为$E$类
1. 在$E$类中选出一个节点$e$，该节点需要满足两个条件：
(1).它和任意$S$类的节点$s$之间存在一条边
(2).对于(1)中所有的边$\left \{ s,e,v \right \}$，权值$v$达到最小
2. 将1中选出的节点$e$归入$S$类
3. 重复执行1，2直到所有节点都为$S$类

接下来，用图给出详细求解过程（红色为$S$类，蓝色为$E$类，绿色为$S$,$E$类节点之间的边）

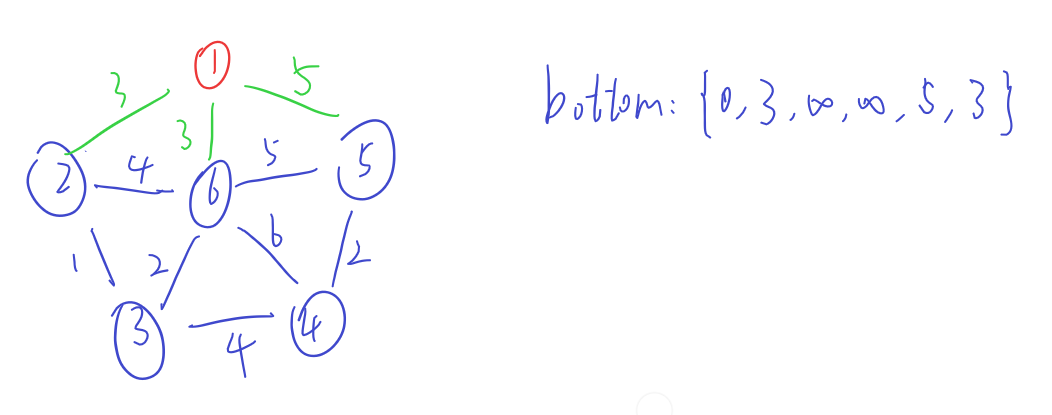
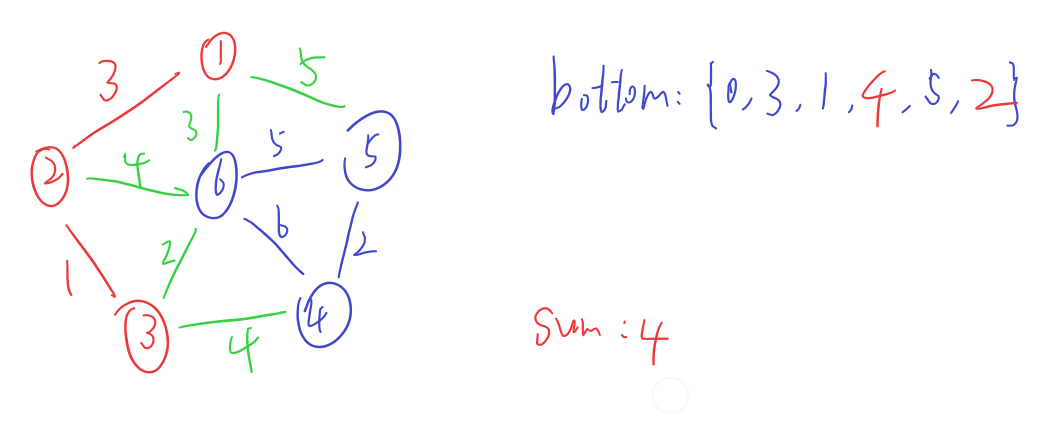
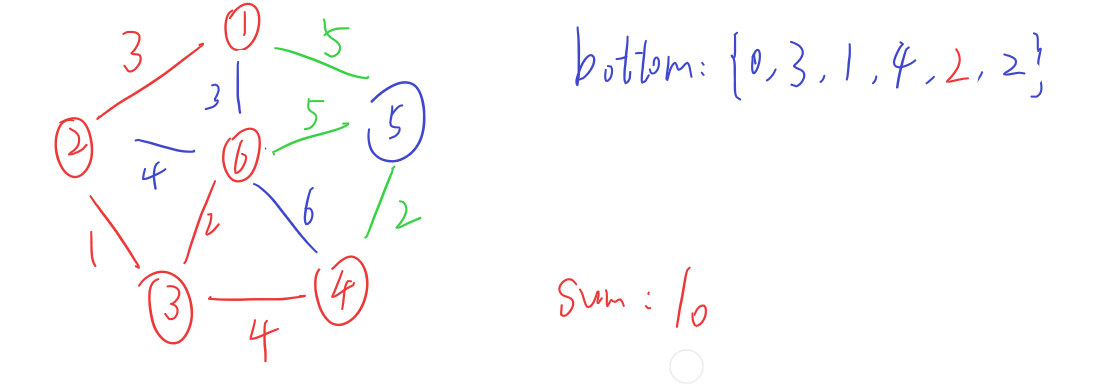
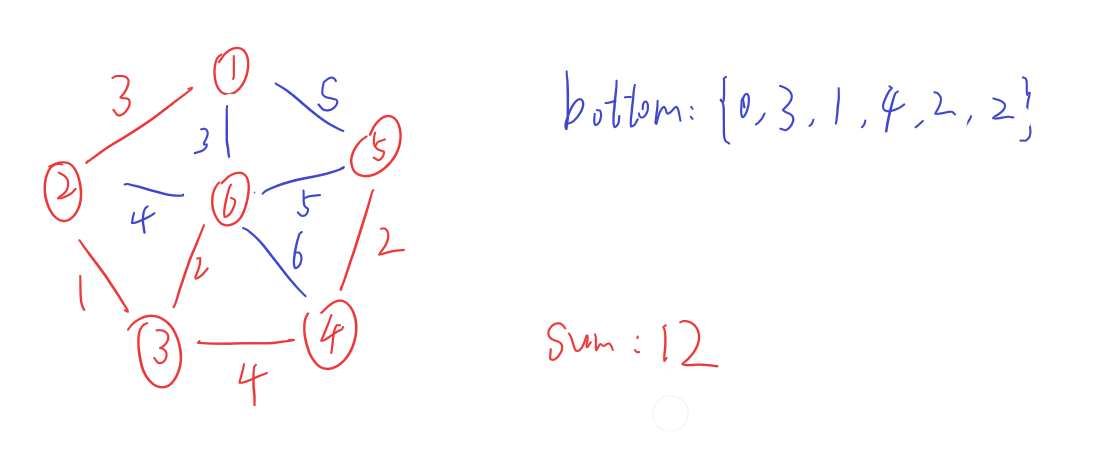
C++ 代码

Prim算法也有两种实现方式，分别基于邻接矩阵和邻接表，下面给出两种实现方式的代码（分别借用之前的MGraph类和ALGraph类）

int MGraph::getSumOfMST(int s) {
    vector<int> visit(numVex + 1),  //记录S类节点
        bottom(numVex + 1, INF);    //记录每个E类节点到任意S类节点的最小边权值
    int ans = 0, cnt = 1;           //需要选取n个节点(s已经在里边了)
    visit[s] = 1;                   //邻接矩阵的实现需要先用s初始化bottom
    for(int i = 1; i <= numVex && i != s; i++) {
        bottom[i] = min(bottom[i], mat[s][i]);
    }
    //再选n-1次
    for(int i = 1; i < numVex; i++) {
        int id = 0, btm = INF;
        //按照步骤1找到合适的E类节点
        for(int j = 1; j <= numVex; j++) {
            if(!visit[j] && bottom[j] < btm) {
                id = j;
                btm = bottom[j];
            }
        }
        //找不到合适的E类节点了，就退出
        if(id == 0) {
            break;
        }
        ans += btm;
        visit[id] = 1;
        cnt++;
        //用刚刚选择过的节点更新bottom表
        for(int j = 1; j <= numVex; j++) {
            if(!visit[j] && bottom[j] > mat[id][j]) {
                bottom[j] = mat[id][j];
            }
        }
    }
    return ((cnt != n) ? INF : ans);    //选不够n个节点，就说明最小生成树求解失败
}

int ALGraph::getSumOfMST(int s) {
    vector<int> visit(numVex + 1), bottom(numVex + 1, INF);
    int ans = 0, cnt = 0;//s不在里边
    //可以借助优先队列实现，优先队列q中Edge的end表示当前选中的E类节点，val表示它到S类节点的距离
    priority_queue<Edge, vector<Edge>, greater<Edge>> q;    
    q.push(Edge(1, 0));//先把s加入
    while(!q.empty()) {
        //首位一定是距离最短的
        Edge edge = q.top();
        q.pop();
        int cur = edge.nxt, value = edge.val;
        if(visit[cur]) {
            continue;
        }
        visit[cur] = 1;
        cnt++;
        ans += value;
        //其余更新与邻接矩阵相似
        for(auto& ed : adjList[cur]) {
            value = ed.val;
            int nx = ed.nxt;
            if(!visit[nx] && value < bottom[nx]) {
                bottom[nx] = value;
                q.push(Edge(nx, value));
            }
        }
    }
    return ((cnt != n) ? INF : ans);
}