先浅浅的整个小暴力做法

首先先试了一下暴力做法哈， 怎么暴力呢
我们可以知道， 在一个矩阵中， 如果说， 我们知道了一个这个矩阵的左上角坐标和右下角坐标，那么我们是可以确定唯一矩阵的， 那么， 如果说我们多设置几层循环，将每个可以形成的矩阵中所有素的加和都遍历一遍， 我们也是有可能找到答案的对吧
当然，纯暴力是有一定的风险的，我们既需要枚举每个矩阵的左上角的纵横坐标
又需要枚举每个矩阵的右下角坐标， 数据范围是 100， 此时最坏时间复杂度已
经达到 10 的八次方了，有较大概率超时的对吧，我们可以浅浅的优化一下，就
是先构造出来一个二维前缀和就好了， 然后根据坐标加减相应的二维子矩阵和，
就可以求得目标子矩阵的和了对吧
ok 上暴力代码

#include <iostream>
#include <algorithm>
#include <limits.h> // INT_MIN 包含于这个头文件中

using namespace std;

const int N = 110;

int n;
int g[N][N];

int main(){
    cin >> n; // 存入n
    // 读入每个元素并构造二维前缀和
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= n; j ++){
            scanf("%d", &g[i][j]);
            g[i][j] += g[i - 1][j];
        }

    //然后直接遍历就好了
    int res = INT_MIN;
    for (int i = 1; i <= n; i ++)
        for (int j = i; j <= n; j ++){
            int last = 0;
            for (int k = 1; k <= n; k ++){
                last = max(last, 0) + g[j][k] - g[i - 1][k];
                res = max(res, last);
            }
        }
    // 输出结果 
    cout << res << endl;

    return 0;
}

更高级的代码就是可以给最坏时间复杂度做到 n 的三次方， 就是 10 的六次方
感觉这个代码就像是降维打击， 给问题从二维讲到一维， ok， 分析一波

一维最大连续子序列之和分析

先从简单分析， 就是当我们有一个一维数组的情况下，我们怎么做， 才能求得
最大的连续子序列的和呢， 具体推理一下哈， 上传个图片

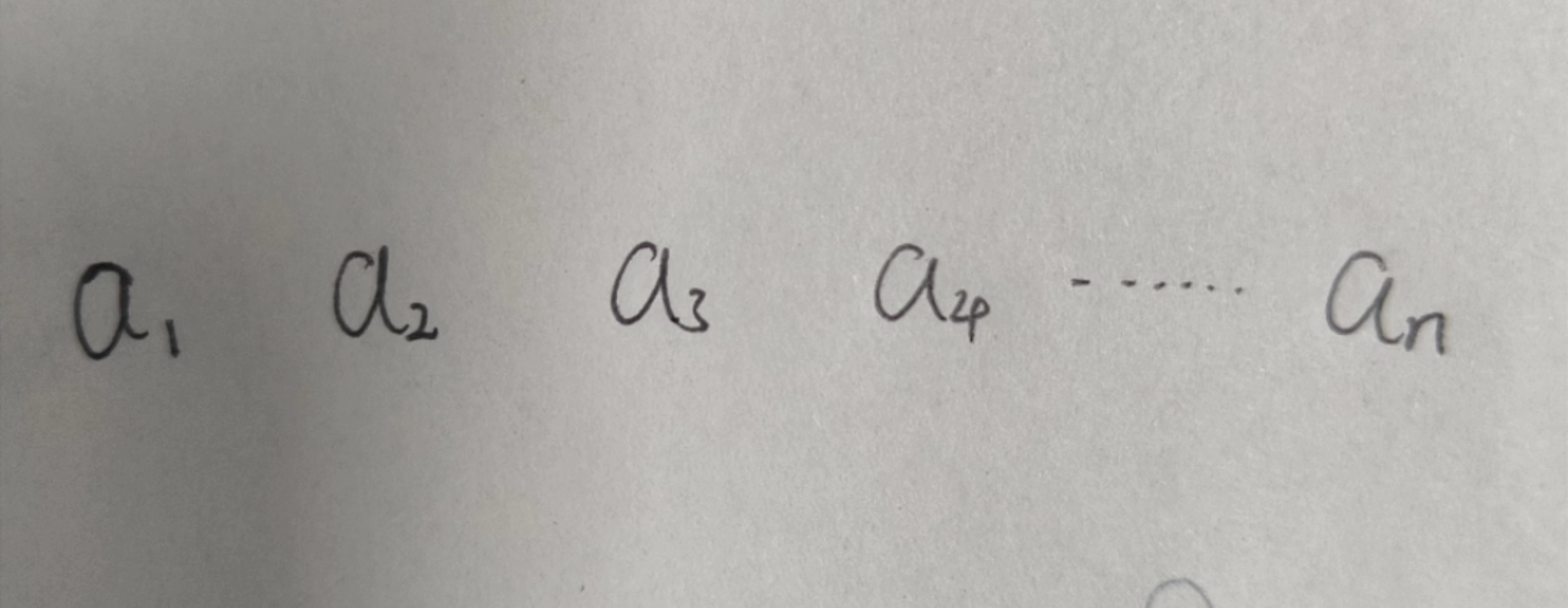
比方说， 现在我们从左到右依次有a1 a2 a3 然后一直到 a n， 现在我们先从a1
来考虑对吧， 当只有a1 时， 那么最大值就是 a1，现在我们考虑 a1 a2 两个数
因为我们要求最大连续子序列的和， 所以， 我们现在不用管 a2 的值的大小及
正负，我们只需要知道加上a1 对其有利还是有害就可以了， 如果说a1 是负值，
那么肯定是有害的， 所以当我们从左到右， 考虑到 a2 时，最大子序列的和就
a2，如果说a1 是正数， 那么从左到右， 当考虑到 a2 时， 最大子序列的和就
是 a1 + a2 了
现在，我们由这两个特殊到一般， 比如， 我们考虑到第 i （i 大于等于2）个
数时， 我们是否要加上前面的数 或 前面的部分数字之和时， 取决于前面的这
个数是正数还是负数， 如果说是正数， 我们肯定要加上的对吧，如果说是负数
就不用管了

从二维到一维

如果说我们现在有一个矩阵，现在我们自上而下，只求得每一列数字的前缀和，
示意图，额，有点丑，大概就是这么个鸟样

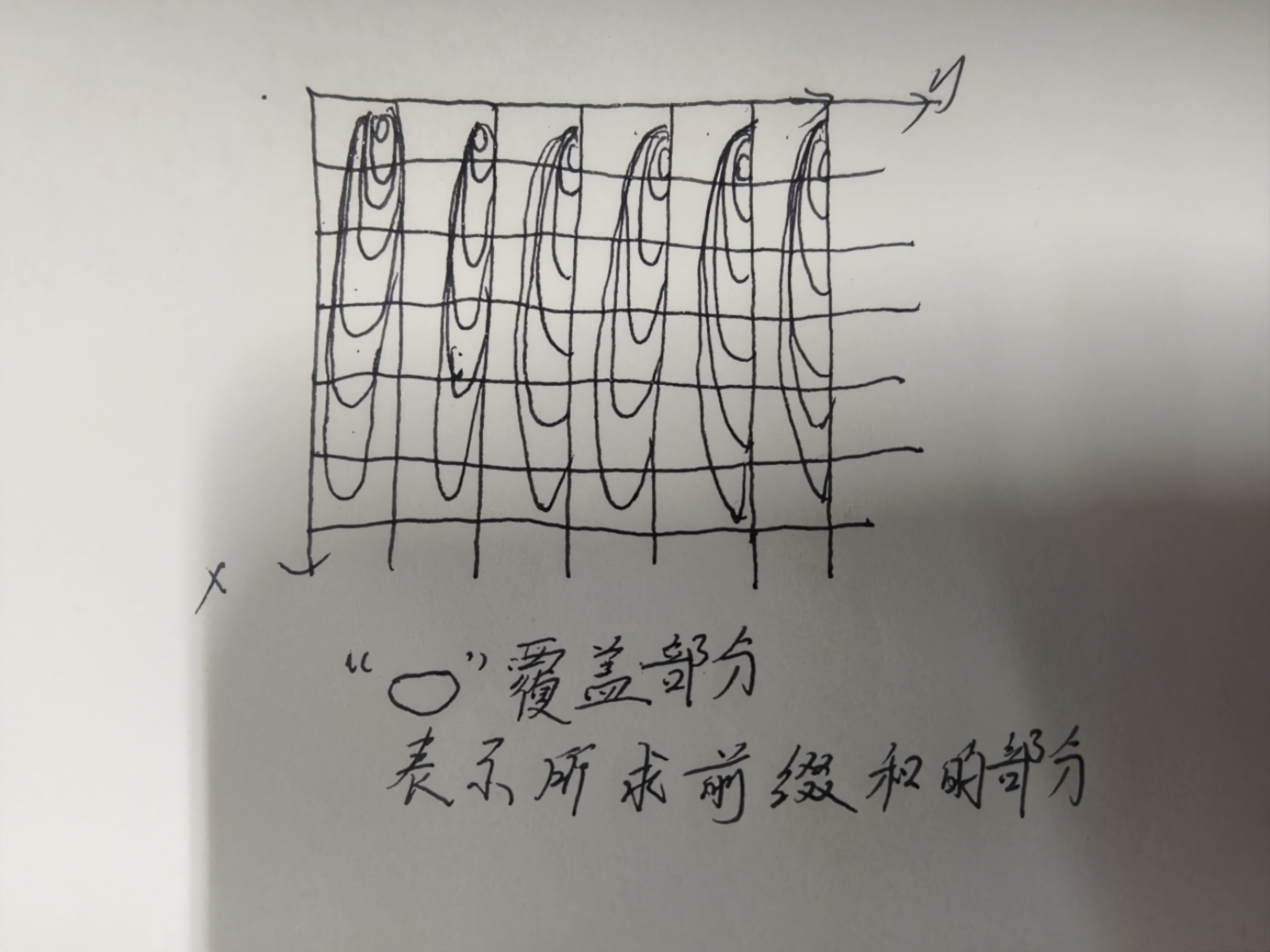
现在， 如果说我们只是枚举一个上界， 一个下界，
然后框出来一定的范围， 就像是这样

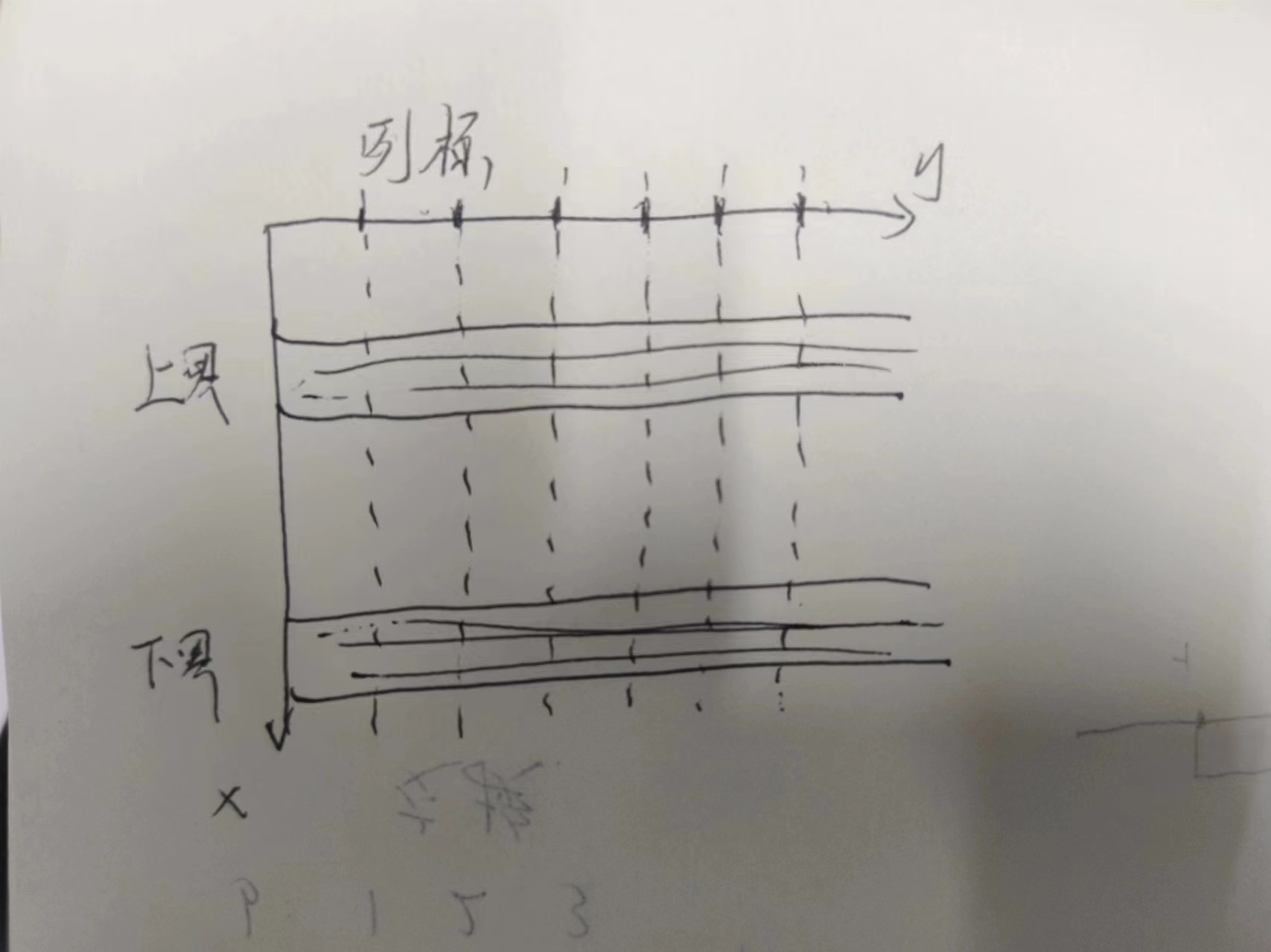
然后再根据列标， 划分成更小的区域，然后再给更小的区域抽象成一维的 a1 a2
a3 一直到 a n 那种，图大概就是这么个鸟样

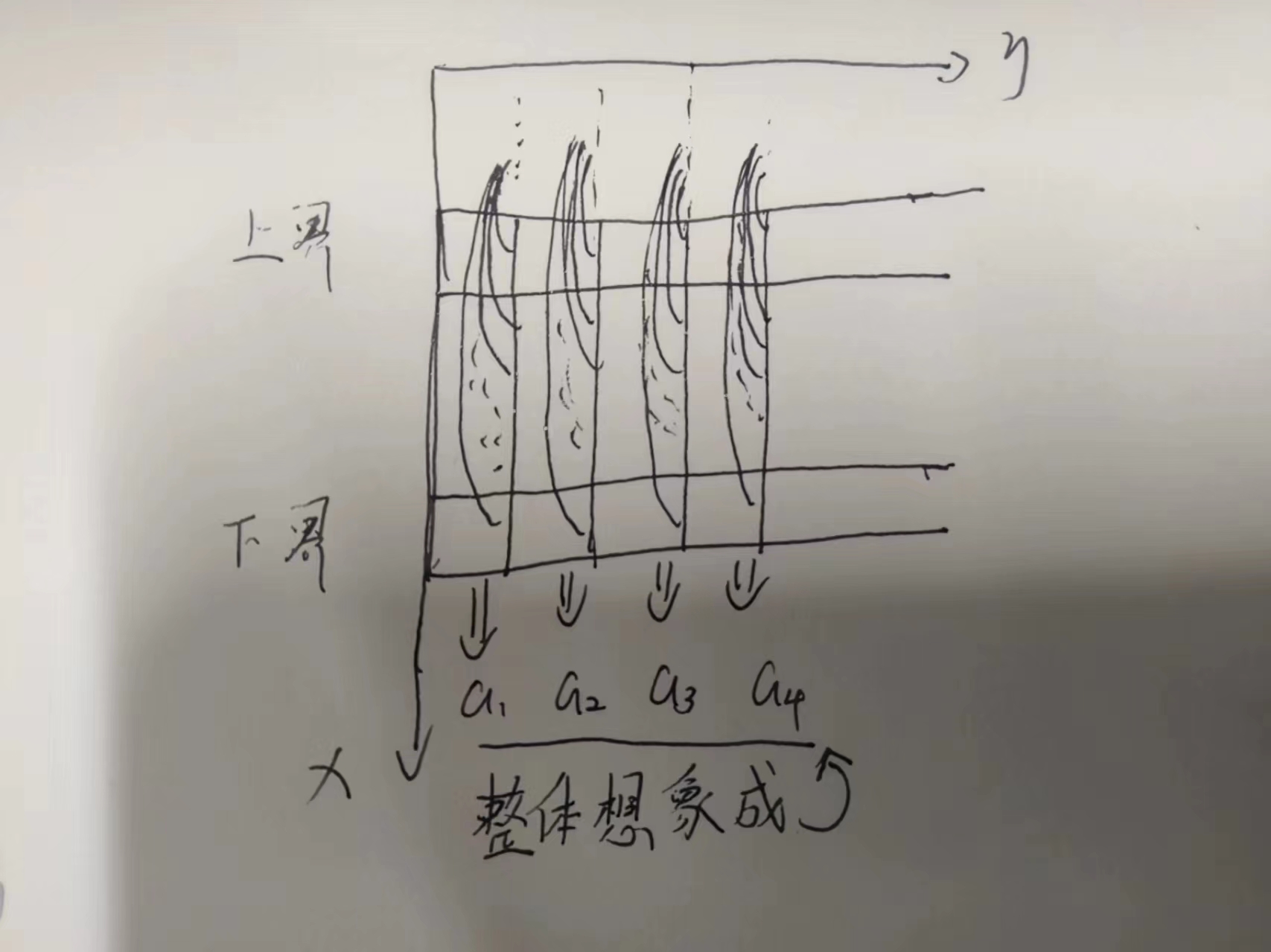
然后我们就可以按照一维的方法去做了，我们需要枚举一个上界，一个下界，还
有就是每一小块区域从左到右的移动，也就是三层循环，最坏时间复杂度是 n 的
三次方， 但是下界的取值依赖于上界的取值，所以最坏时间复杂度是到不了 n
的三次方的

需要注意的是对 “各列前缀和的处理”， 就像是截取部分子序列的前缀和
ok， 终于到了上代码环节

#include <iostream>
#include <algorithm>
#include <limits.h>

using namespace std;

const int N = 110;

int n;
int g[N][N];

int main(){
    cin >> n;
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= n; j ++){
            scanf("%d", &g[i][j]);
            g[i][j] += g[i - 1][j];
            // 构造每列前缀和
        }

    int res = INT_MIN;
    for (int i = 1; i <= n; i ++)
        for (int j = i; j <= n; j ++){
            int last = 0;
            for (int k = 1; k <= n; k ++){
                // last 就像是前面的那个数值， 然后跟 0 比较
                // 如果大于 0， 就加上， 否则就不用管了
                last = max(last, 0) + g[j][k] - g[i - 1][k];
                // 上面这一行代码的后半部分主要就是对各列前缀和的截取
                // 就是那个抽象出来的 a[k]
                res = max(res, last);
            }
        }

    cout << res << endl;

    return 0;
} 

这个运行时间比上面那个运行时间快了将近 20 倍了 ！！！