$\Huge\color{orchid}{点击此处获取更多干货}$

并查集

并查集是处理“不相交集合”的专用数据结构，对于每一个集合，其存储方式类似于树结构。每个集合都需要选取一个代表元素，此后就可以用它来标识整个集合，两个针对集合的主要操作“合并”和“查找”都需要借助这些代表元素实现。

下图中展示的，就是并查集中集合和元素的存储结构：

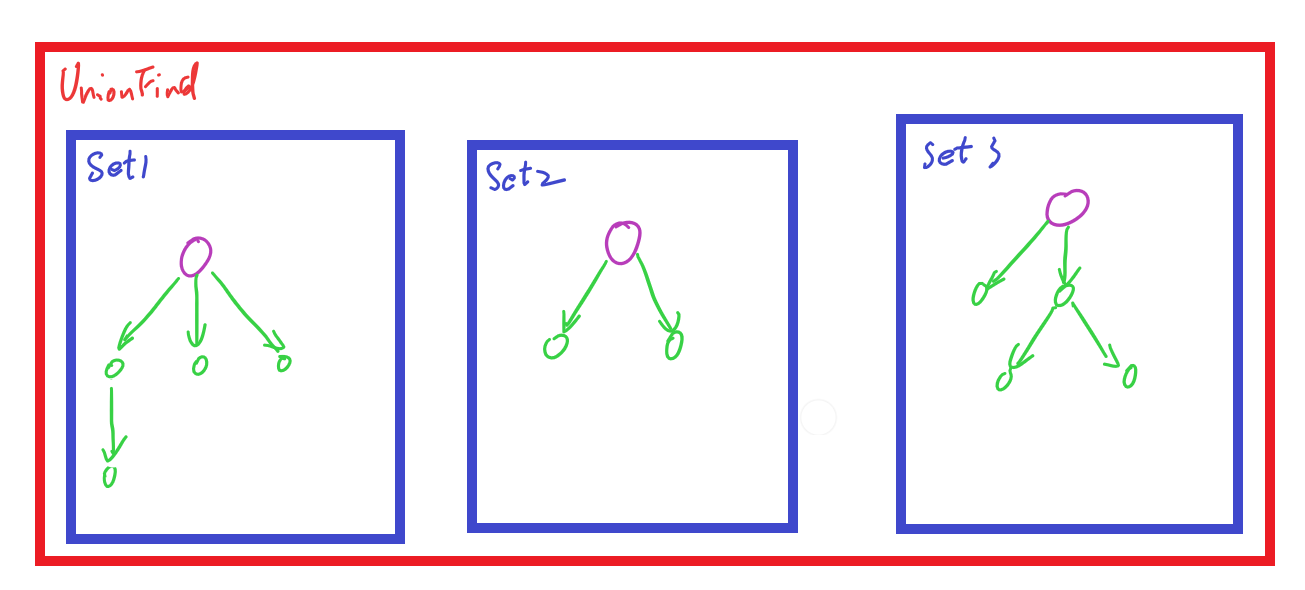
红色方框代表整个并查集($\text{UnionFind}$)结构，内含的蓝色方框就代表其中的每个“不相交集合”($\text{DisjointSet}$)，这些集合全都是由树结构存储的。这些树结构中的节点就相当于集合中的元素，紫色节点相当于集合代表元素，而其他的绿色节点就是集合中一般元素。换言之，一个集合中每个绿色元素，都可以直接或间接的由紫色元素衍生而来，对于其余绿色节点，其在对应的树结构中的父节点，相当于这个元素的源($\text{origin}$)。以上可结合类之间的继承、派生关系相互类比理解。

接下来将会结合代码，介绍并查集的初始化，以及“并”和“查”操作

C++ 代码

并查集类声明如下：
虽然集合元素可以是任意的，但408数据结构中只定义了整数1~n，这些可以作为数组下标，帮助我们用索引代替指针实现树结构

class UnionFind {
private:
    int* origin; //重要的只有元素的“源”，因此只需要源索引就够了
public:
    //包含n个元素的并查集构造函数
    UnionFind(int n);

    //析构函数
    ~UnionFind();

    //“查”操作，查找元素e对应集合的代表元素
    int find(int e);

    //“并”操作，将元素x和元素y对应的集合合并起来（注意C++中union是关键字，不能用于函数名）
    void unite(int x, int y);
};

初始化时，由于还没有经过任何合并操作，每个元素自身都代表一个独立集合，它们的源都是自身，以后规定源和自身相同的元素为集合代表元素

UnionFind::UnionFind(int n) {
    origin = new int[n];
    //iota作用是为序列某区间进行递增赋值
    //这里的效果就是初值为0，为origin数组递增赋值，使得每个位置的元素值等于下标
    iota(origin, origin + n, 0);
}

UnionFind::~UnionFind() {
    delete[] origin;
}

如果不进行任何改进，存储一个集合的树可能是一条链，这样时间效率就会比较低，改进的方法有两种，这次先介绍针对“查”的改进：路径压缩

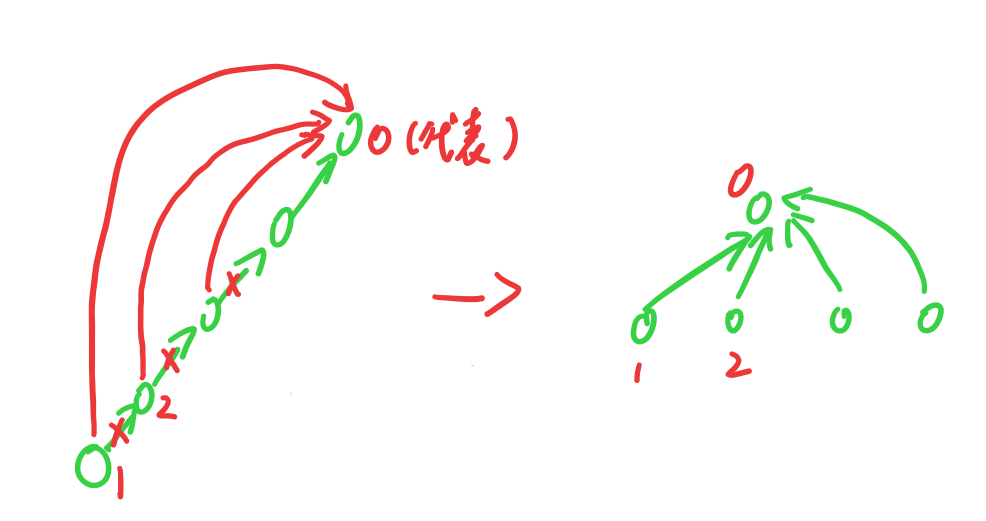
集合中代表元素是最上面的元素0，整个集合形似一条链表，元素1和元素2则位于链表的最末尾，这样的话从元素1查找到元素0，就相当于要遍历整个集合。改进的方式就在于将它的源，也就是图中元素2所在集合的代表元素0，重新设置为它的源。对于集合中的其他元素也有相同的做法，效果就是将每一个元素的源都集中为本集合的代表元素。在代码中，这个改进可以借助递归实现。

int UnionFind::find(int e) {
    if(e != origin[e]) {            //非代表元素全都要压缩路径
        int ori = find(origin[e]);  //递归方式找到集合代表元素
        origin[e] = ori;            //重新设置e的源
        //两个操作可以合并为一行origin[e] = find(origin[e]);
    }
    return origin[e];               //经过路径压缩后可以保证e的源就是所在集合的代表元素
}

最后的合并操作其实已经呼之欲出了，按照“查”的方法找到两个集合的代表元素后，让其中一个成为另一个的源即可。

void UnionFind::unite(int x, int y) {
    int pr = find(x), nx = find(y); //对应prev,next
    if(pr == nx) {                  //代表元素相同，意味着两个元素已经在同一集合中
        return;                     
    }
    ori[pr] = nx;                   //“后一个”成为“前一个”的源
}