如果说我们想最快完成任务，那么，我们肯定不能采取一段一段的铺设道路
我们因该尽可能连续性的铺路，即一次性铺设多段道路

在铺设道路时， 我们可能会遇到几种情况

单峰情况

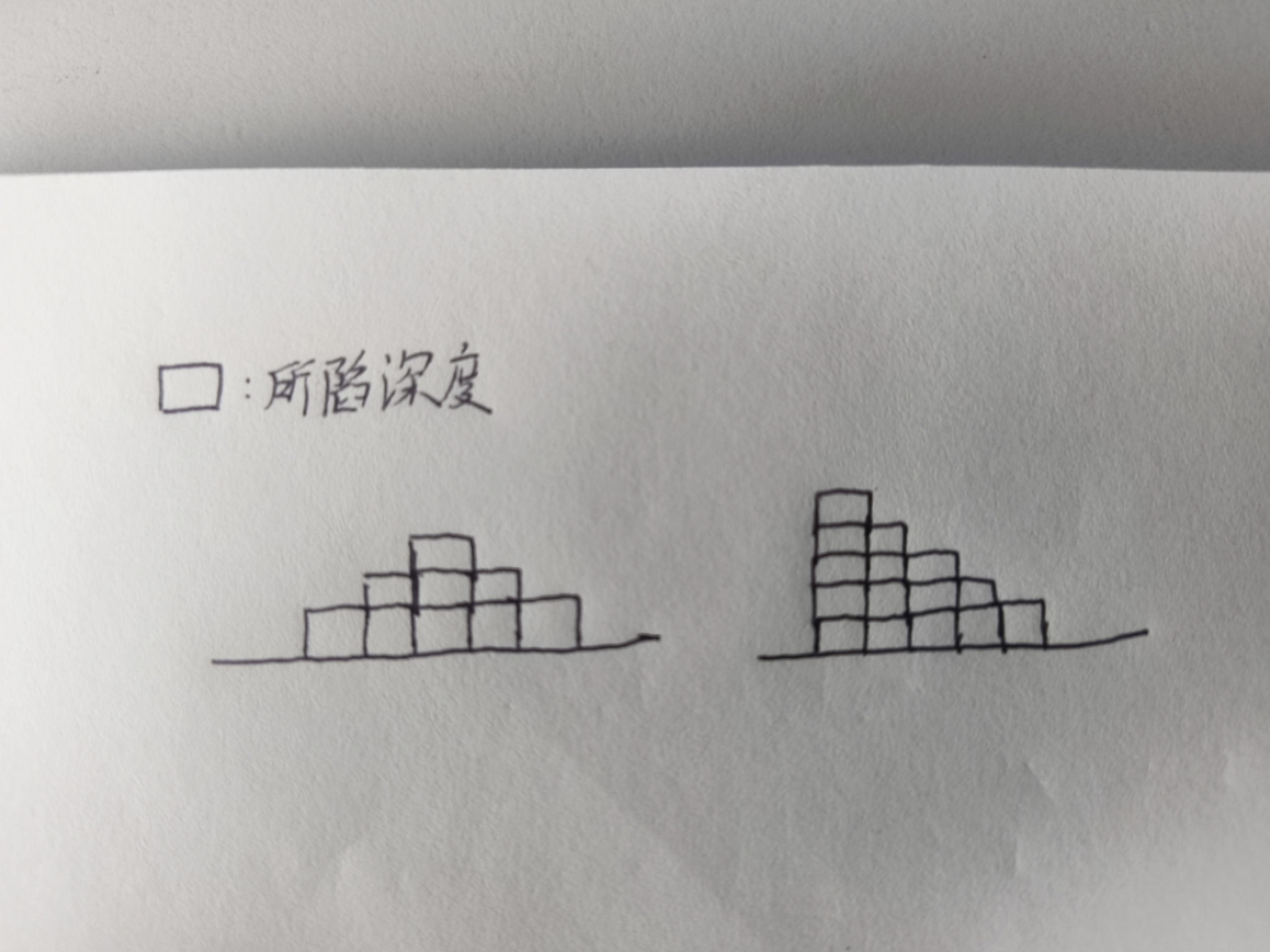
如图所示，在一段连续区间内，出现了“峰”的情况， 那么在该连续区间，如果
想给道路完全填平，就取决于最高“峰”的高度
感觉右侧的情况更契合下面的推理过程

多峰情况

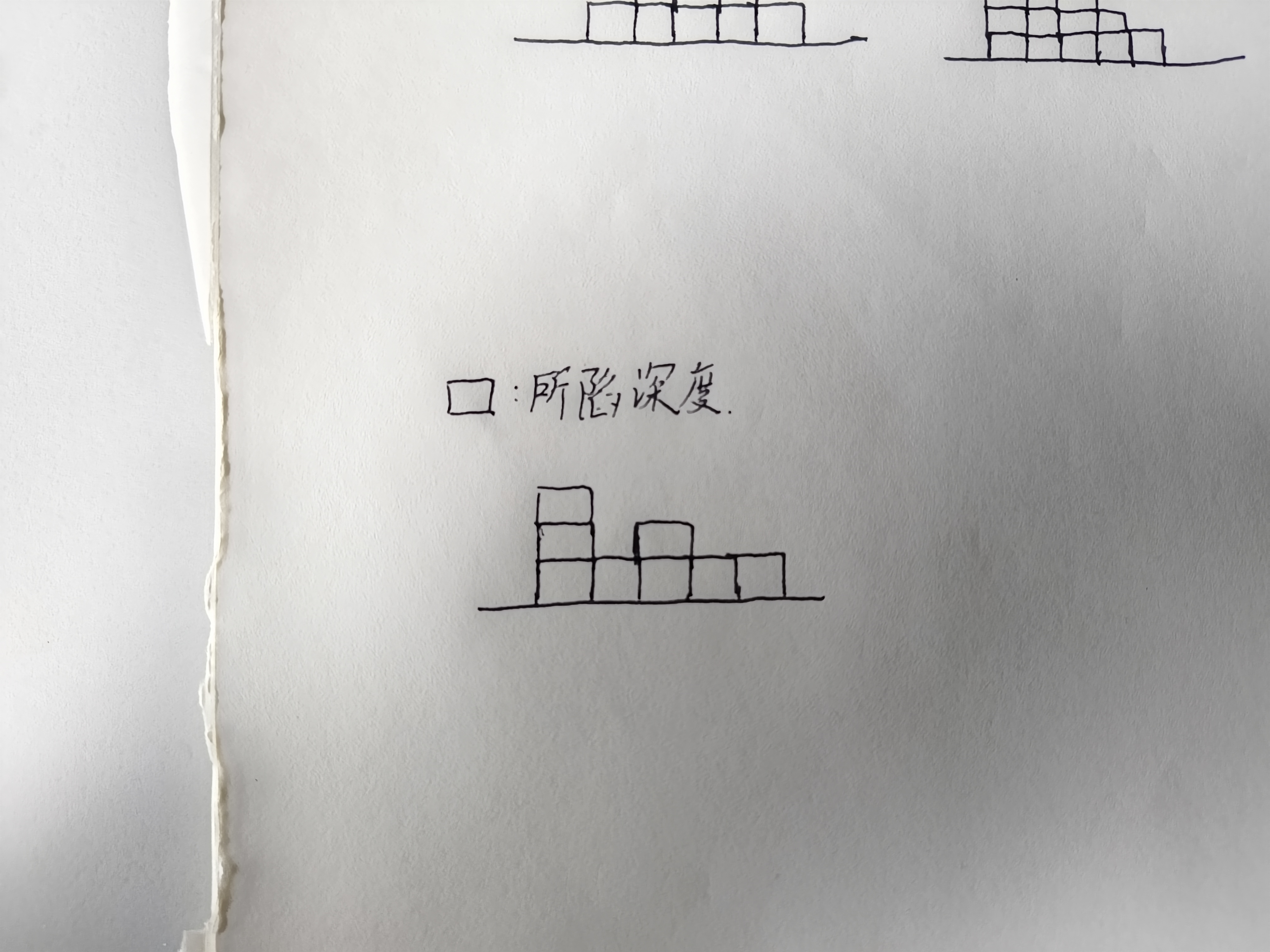
此种情况应该算是比较贴合实际的，我们一般都是由特殊到一般，现在
我们拿出现两个“峰”的情况举例
如果说在一段连续区间内， 出现了两个“峰”，那么在比两“峰”都低的地方
被填平后，二者会断开，二者需要分别被填平

现在我们可以根据想法进行推理， 设f[i] 表示到达 第i 段路时， 前面
所有路被填平需要花费 f[i] 天，a[i] 表示每段路需要被填平的深度
如果说，前面一段路需要填平的深度此段路大，即“单峰情况”（参照图
一 右），则此段路包括此段路之前的路段完全被填平的时间等于此段路之
前的路完全被填平所需要的时间
如果说，前面一段路需要填平的深度比此段路小，即“多峰情况”，则此段路
之前的所有路段，包括此段路被完全填平所需要的时间就等于 此段路之前
所有路段被完全填平所需要的时间 加上 此段路于前一段路所需要被填平深
度的差值

此策略基本上就是相当于从头遍历一遍，时间复杂度大概是 O(n)

上代码

#include <iostream>

using namespace std;

const int N = 100010;

int a[N], f[N];

int main(){
    int n;
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);

    f[1] = a[1]; // 起始是 f[1] = a[1]
    for (int i = 2; i <= n; i ++) // 从2开始遍历
        if (a[i - 1] > a[i]) f[i] = f[i - 1];
        else f[i] = f[i - 1] + a[i] - a[i - 1];
    printf("%d\n", f[n]);

    return 0;
}

可以对空间进行优化， 时间上优化不太明显
优化版本代码如下

#include <iostream>

using namespace std;

const int N = 100010;

int a[N];

int main(){
    int n;
    scanf("%d", &n);

    for (int i = 1; i <= n; i ++)
        scanf("%d", &a[i]);

    int res = a[1];
    for (int i = 2; i <= n; i ++)
        if (a[i - 1] < a[i]) res += a[i] - a[i - 1];

    printf("%d\n", res);

    return 0;
}