$\Huge\color{orchid}{点击此处获取更多干货}$

SPFA

Bellman-Ford算法复杂度过高，究其原因主要是涉及了很多无效操作，如下图所示：

第一轮迭代中，有效的边只有$\left \{ 1,2,1 \right \} $，剩余的都是无效操作，特别是对边$\left \{ 3,4,-9 \right \} $，无穷减去9仍然趋于无穷。只有在节点2的最短距离确定之后的第二轮迭代中，$\left \{ 2,3,10 \right \}$和$\left \{ 2,4,10 \right \}$才会有用。最短距离未被更新过的节点，对其后继节点更新最短距离是无效操作，在SPFA算法中，避免这样的无效操作成为了核心。

与上述核心思想对应的，每次更新时，只会对有效节点的后继节点执行松弛操作，因此可以像BFS那样，用队列保存有效节点。除此之外还有一层去重，那就是因为在SPFA算法中，同一个节点不会被反复更新，因此还要留意每个节点是否已经在队列中。松弛操作成功执行，并且不在队列中的节点才需要加入队列

有了上述两层优化，SPFA的平均时复可以降到$O(m)$，其中时间函数$T(m)$与有向边数$m$的关系满足$\lim_{m \to \infty} (T(m)/m) = k \le 2$，也是所谓的$O(k*m)$的由来。但是SPFA跟考研数据结构中用端点作为枢值的快速排序一样，时间复杂度不稳定，最差情况下还是有可能达到$O(n*m)$的，以下是几种可能会让SPFA达到此复杂度的情况，可自行模拟（源点全都是1）：

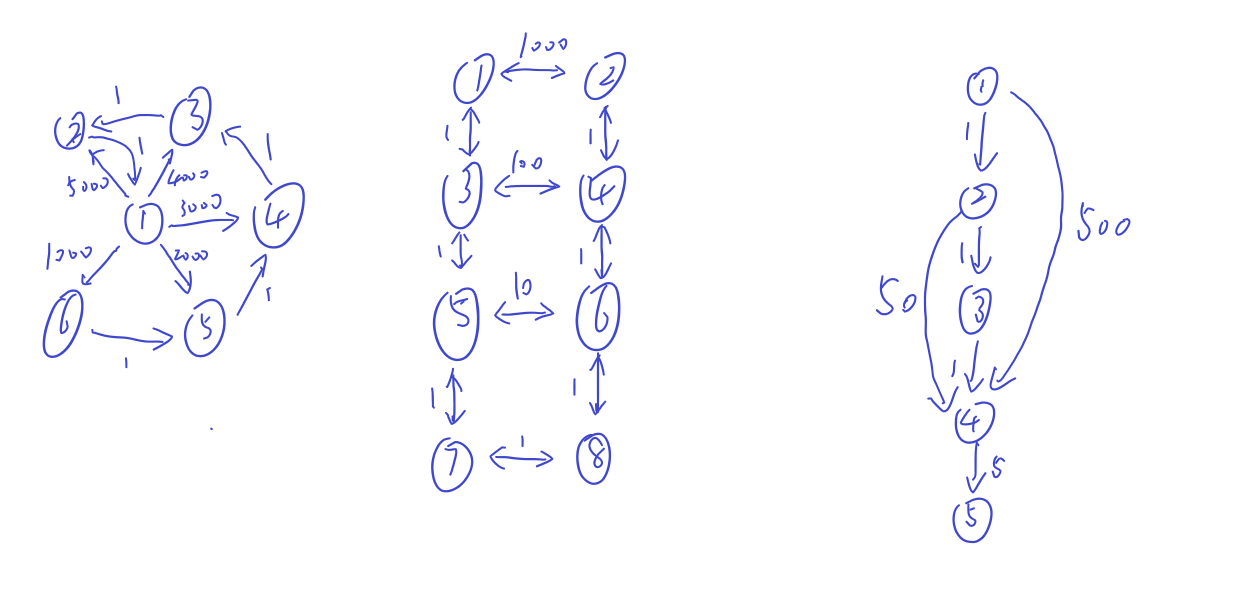
结合前段时间出现的一句论断“SPFA已死”，给出一条重要建议：图中无负权值边，不建议用SPFA

C++ 代码

LinkGraph类来自前置知识

vector<int> LinkGraph::shortestDistance(int s) {
    vector<int> dists(numVex + 1, 1e9 + 7),     //距离表
                inQueue(numVex + 1);            //是否在队列中
    queue<int> q;
    dists[s] = 0;
    //源点加入队列
    q.push(s);
    inQueue[s] = 1;
    while (!q.empty()) {
        int cur = q.front();
        q.pop();
        inQueue[cur] = 0;
        //只更新后继节点
        for (int i = last[cur]; i != 0; i = prev[i]) {
            int nx = fin[i];
            if (dists[nx] > dists[cur] + val[i]) {
                dists[nx] = dists[cur] + val[i];
                //松弛成功，但已在队列中，就不需要反复入队列了
                if (!inQueue[nx]) {
                    inQueue[nx] = 1;
                    q.push(nx);
                }
            }
        }
    }
    return dists;
}