$\Huge\color{orchid}{点击此处获取更多干货}$

Bellman-Ford算法

有限路线单源最短路问题虽然可以由Dijkstra算法衍生而来，但是Dijkstra算法的一个硬伤不可忽略：无法处理带负权值边的图，如下图所示：

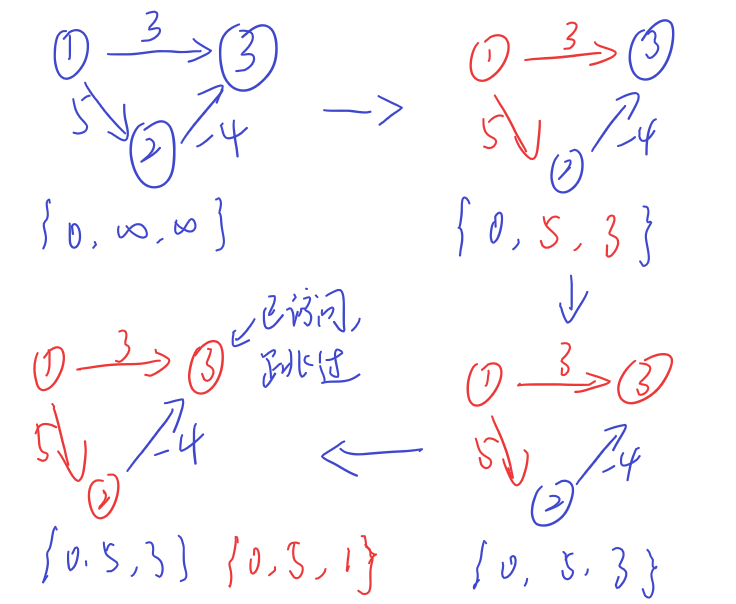
很明显，结果出现了错误，由于Dijkstra算法的贪心性质，忽略了负权值边{2,3,-4}，这个时候就得请出本期主角：Bellman-Ford算法

如果不限制经过边的数量，由于最短路径本身就具有边数量上限n-1，Bellman-Ford算法可以直接迭代n-1次，实际上其迭代次数$i$，相当于求出了从源点到所有节点，经过不超过$i$条边的，因为Bellman-Ford算法每一轮迭代，做的事情就是遍历每条边${src, des, val}$并按照$dists[des] = min(dists[src] + val, dists[des])$来更新。换一种思路，假设$d(i, j)$代表从源点到节点$i$，最多经过$j$条边的最短距离，那么可用下面的图表来表示：

由于$d(i,j)$的值只会由$d(i,j-1)$的值转移而来，因此可以使用另一条与dists等长的数组last来表示，迭代的过程中就借助此数组来滚动
上面的图表，在以后的动态规划部分中会经常出现

C++ 代码

Bellman-Ford算法对图结构有特殊存储方式，因此不再借用前置知识中的图类

struct Edge {
    //每条边按照{起点，终点，权值}独立存储
    size_t src = 0, des = 0;
    int val = 0;
    Edge() {}
    Edge(size_t s, size_t d, int v) : src(s), des(d), val(v) {}
};

class BFGraph {
private:
    vector<Edge> edges;         //所有的边
    vector<int> last, dists;    //滚动数组，last代表上一轮结果，dists代表当前轮结果
    const int INF = 1e9 + 7;
public:
    BFGraph(int n, int m) {
        dists.resize(n + 1, INF);
        size_t s, d;
        int v;
        while(m--) {
            cin >> s >> d >> v;
            edges.emplace_back(Edge(s, d, v));
        }
    }

    //从节点s开始，经过不多于k条边的最短距离
    vector<int> shortestDistance(int s, int k) {
        dists[s] = 0;
        //进行最多k次松弛，第i轮松弛的结果为从起点到每个节点，经过不多于i条边的最短距离
        for (int i = 0; i < k; i++) {
            last = dists;   //以此来滚动
            for (auto& e : edges) {
                dists[e.des] = min(dists[e.des], last[e.src] + e.val);
            }
        }
        //将所有不可达节点的距离重新标记为负无穷，便于类外判断
        for_each(dists.begin(), dists.end(), [&](int& d)->void {
            //考虑到负权值边的情况，d是有可能缩小的，但1e9-5e6也不会小于5e8(INF/2)
            if (d >= INF / 2) { 
                d = INT_MIN;
            } 
        });
        return dists;
    }
};