现在我们假设有n 个小朋友围在一起， 如图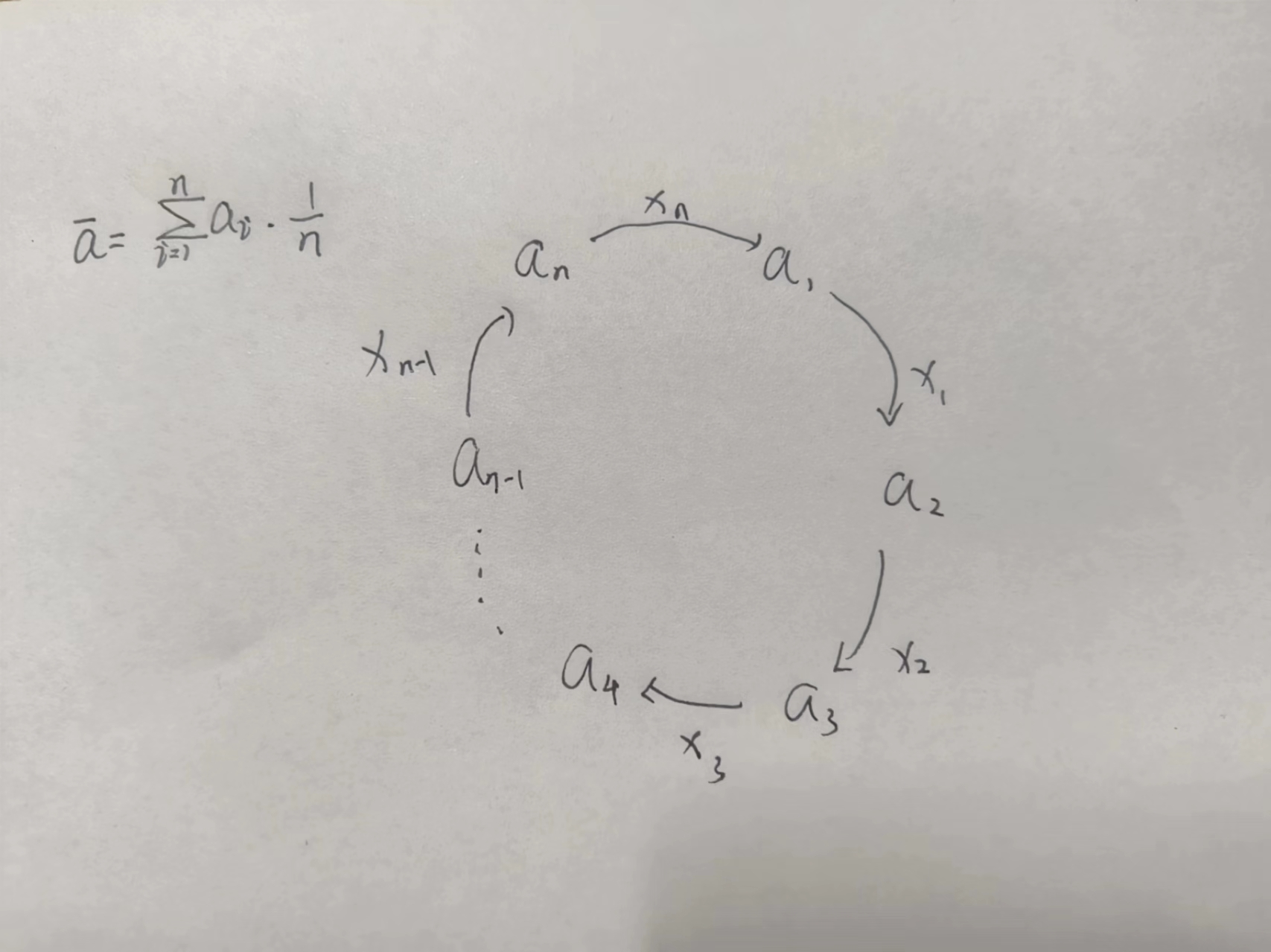
并设第 i 个小朋友有 a[i] 个糖果，设 a拔 为所有小朋友拥有的糖果数
量之和的平均数
现在我们假设 第 i 个小朋友给第 i + 1 个小朋友 x[i] 个糖果， 第
n个小朋友给第一个小朋友 x[n] 个糖果， x[i] 的数值可正可负， 当
x[i] 的值为负数时， 表示第 i 个小朋友给第 i + 1 个小朋友要了
x[i] 个糖果
因为题目一定有解， 所以这么一圈交换下来之后， 肯定是可以让每
个小朋友拥有的糖果数量相同， 也就是说所有 x[i] 的绝对值之和一
定有解， 但是并不一定有唯一解
我们可以拿题目中的样例来举例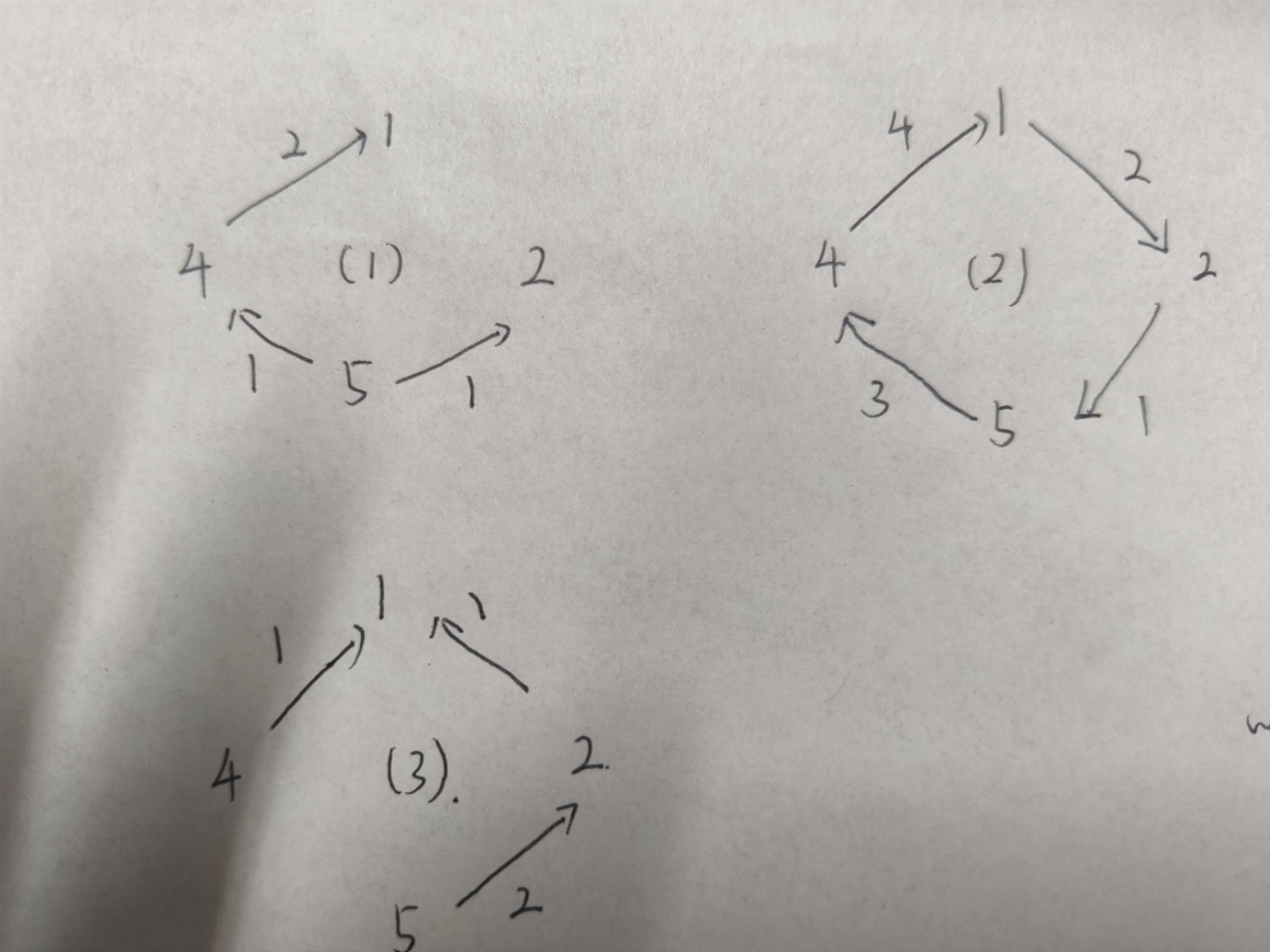
如果说， 我们想寻找最优解话， 肯定不会像是 (2) 那样， 拥有五
个糖果的小朋友多给了， 也就是说， 如果我们想寻找最优解， 至少
有两个相邻的小朋友之间没有糖果的转移， 也就是说， 存在 x[i] = 0
换句话说就是形不成闭环
现在我们可以试着写一下推导

当我们拥有 n 个未知数并且我们拥有 n 个状态描述方程时， 我们可
以求出每个未知数的大小， 但是本题由上述推断可知， x[i] 的值是
无法确定的， 也就是说至少有一个状态描述方程是无效的
但是，不难看出，我们可以用其中一个未知数， 来表示其余的未知数
也就是说， 我们可以将每个 x[i] 的绝对值之和， 用含有一个未知
数的函数表达式来表示， 现在， 我们拿 x[1] 来作为那个未知数
如图

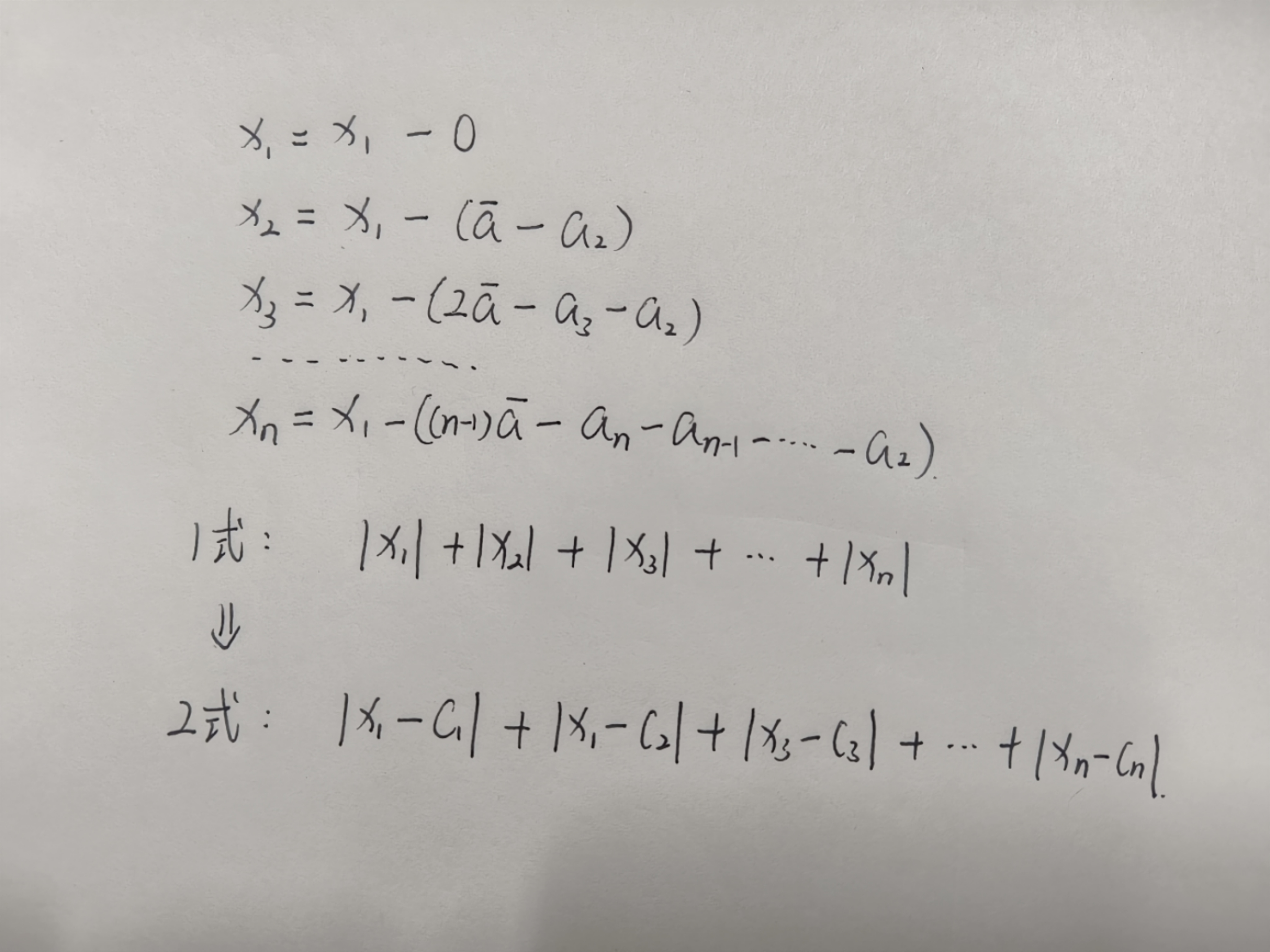
然后可以看出来，每个 x[i] 都可以用 x[1] 减去一个常数 c 来表示
现在， 我们求解答案的式子由 1式 转变成了 2式
2式 就类似于从数轴上选一个点， 使得该点到坐标轴上相关点的距离
之和最小
现在， 我们可以整理一下 c， 如图

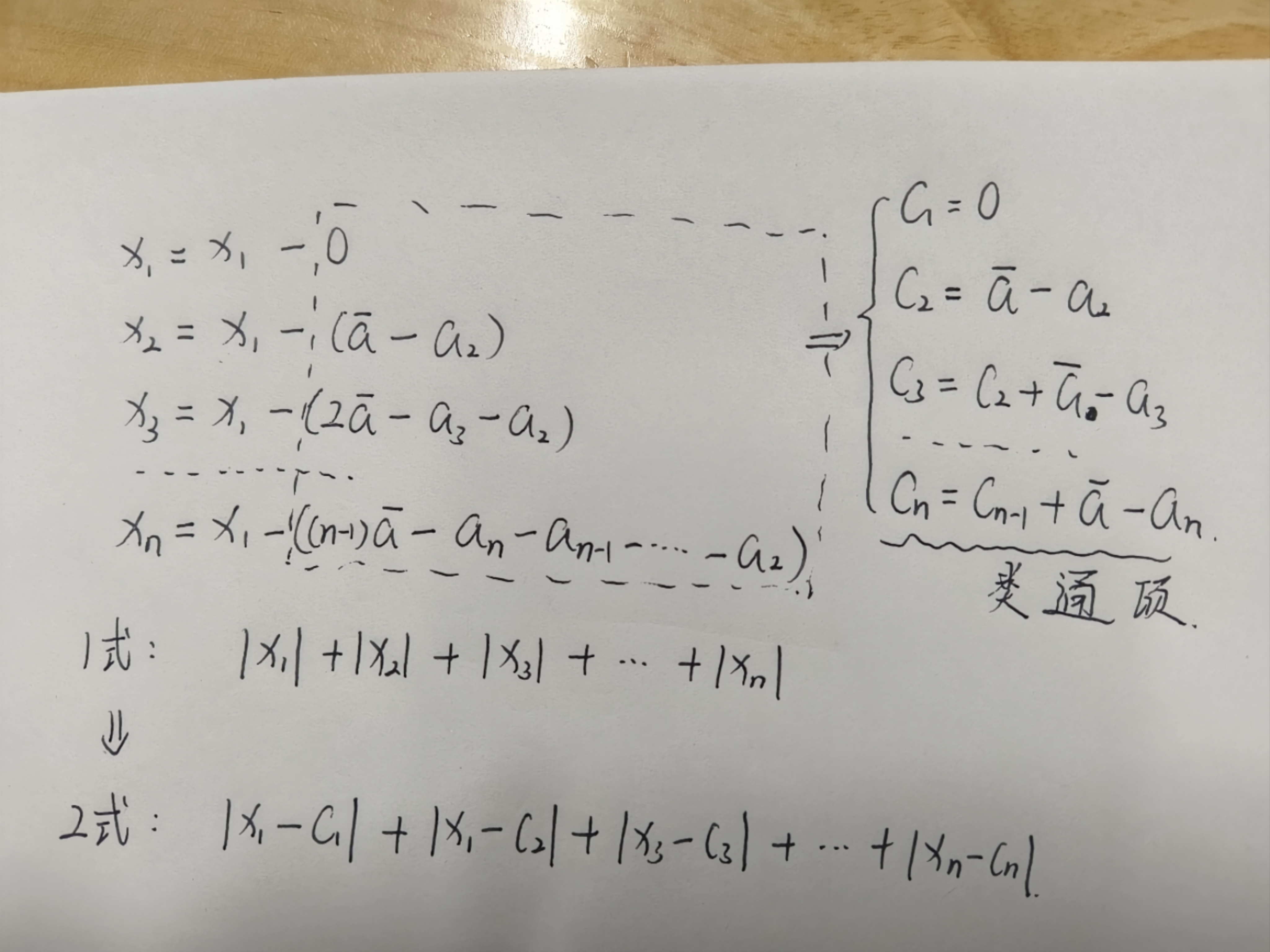
然后， 我们可以给 c[i] 排序， 然后按照 仓库选址 的写法来解题了

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;
// 数据范围较大，有的数据用 long long 来定义

const int N = 1000010;

int a[N]; // 存储每个小朋友初始时拥有的糖果数量
LL c[N];  // 存储处理过后， 减去的常数

int main(){
    int n;
    scanf("%d", &n);

    LL sum = 0; // 求平均数时， 先求出来总共的和是多少
    for (int i = 1; i <= n; i ++){
        scanf("%d", &a[i]);
        sum += a[i]; 
    }
    LL avg = sum / n; // 计算 a拔 是多少

    c[1] = 0; // 初始 c[1]， 其实没必要， 因为 c 数组是全局变量
    for (int i = 2; i <= n; i ++)
        c[i] = c[i - 1] + avg - a[i];
        // 处理每一个常数

    sort(c + 1, c + n + 1); // 给常数排序

    int mid = c[(n + 1) / 2]; // 找出中位数是多少
    LL res = 0; // 定义答案
    for (int i = 1; i <= n; i ++)
        res += abs(c[i] - mid); // 求每一项的绝对值

    printf("%lld\n", res); // 输出结果

    return 0;
}
其实我有点好奇， 刚刚这个代码是因为数组没有开够，
然后 segmentation fault 了， 但是给数组开够了， 调试
代码， 结果不对， 但是提交通过了， 嘶 ~