题目描述

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

样例

输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
8

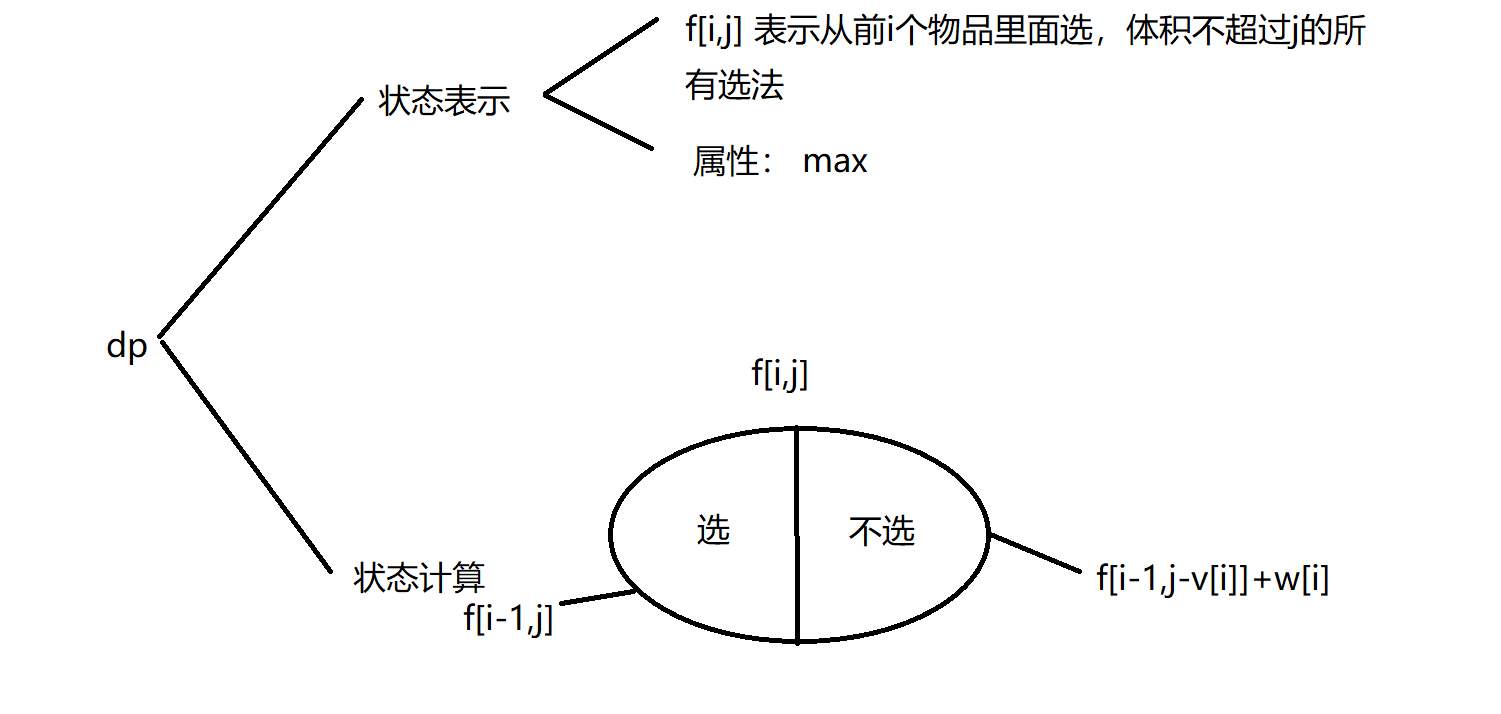
朴素版dp

状态转移用到i-1，所以i从1开始

初始状态为f[0][j]=0

选第i个物品没有直接的状态可以表示，故使用f[i-1j][j-v[i]]+w[i]表示

时间复杂度$O(n^2)$

#include<iostream>
using namespace std;
const int N=1010;
int w[N],v[N];
int f[N][N];
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
        }
    cout<<f[n][m]<<endl;
    return 0;
}

空间优化版

状态表示从二维优化到一维，通过观察注意到，i只使用到i-1的状态，所以表示i的这一维可以去掉

#include<iostream>
using namespace std;
const int N=1010;

int f[N],w[N],v[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)       //将空间优化到一维后选第i个物品状态表示f[i]=f[i],故直接省略
        for(int j=m;j>=v[i];j--)//如果从小到大枚举体积，f[j-v[i]]表示的是选第i个物品的状态，而不是i-1个物品状态
            f[j]=max(f[j],f[j-v[i]]+w[i]);

    cout<<f[m]<<endl;
    return 0;
}