$\Huge\color{orchid}{点击此处获取更多干货}$

Dijkstra算法

Dijkstra最短路算法非常重要，至少是考研数据结构的巨头之一，有的时候甚至会和计算机网络来个学科交叉（比如2014年408的42题）。由于本篇是第一次引入最短路概念，故对于最短路的求解过程，会来个详细展开

如果用$d(x)$表示起点到某个节点$x$的最短路，$v(i,j)$代表直连节点$i,j$的边，那么Dijkstra最短路算法分为以下几步：
1. 初始化$d(s)=0$
2. 在未访问节点中选择距离起点最近的节点$x$
3. 访问节点$x$并更新其后继所有节点的最短路，对于每一个后继节点$y$，如果$d(y)>d(x)+v(x,y)$，那么就令$d(y)=d(x)+v(x,y)$（进行一轮松弛操作）
4. 重复执行步骤2，3共$(n-1)$次

下面是详细执行过程：（红色代表当前轮访问和修改的信息，绿色表示此后不需要再修改的信息）
初始化：（1为源）

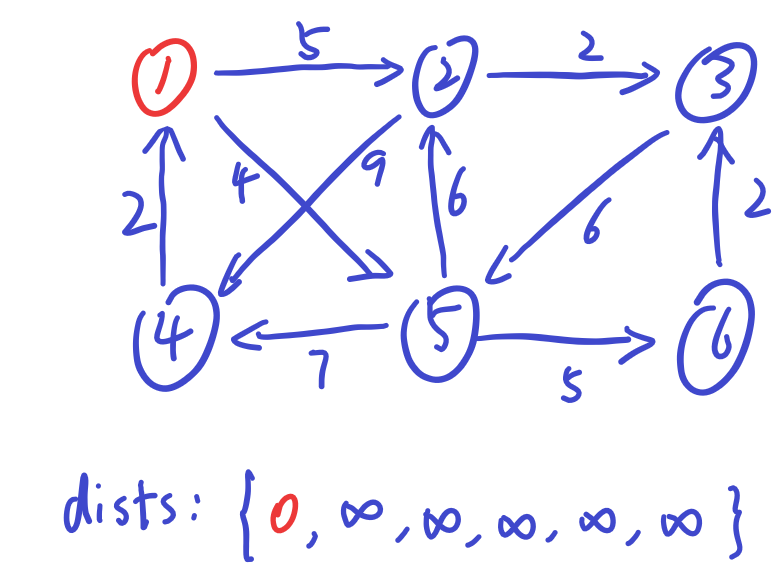
$d(x)_{max}=d(1)=0$，选择节点1

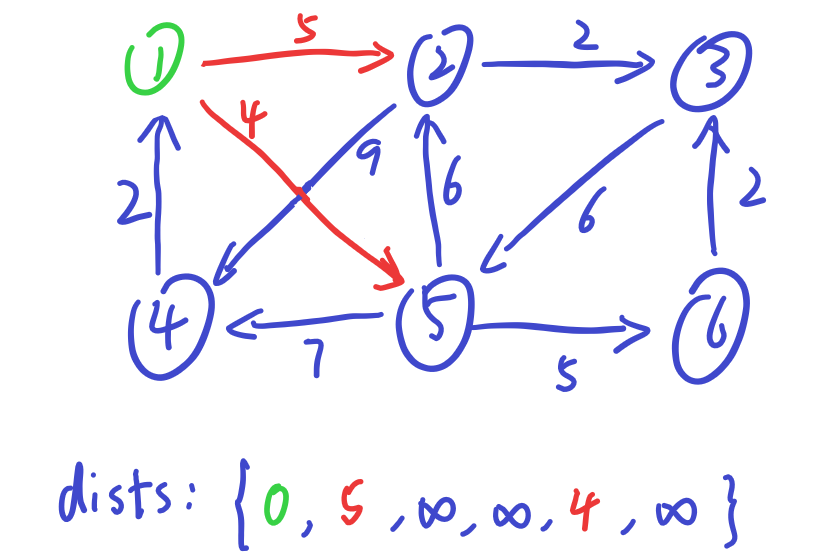
$d(x)_{max}=d(5)=4$，选择节点5，由于$d(2)<d(5)+v(5,2)$，故$d(2)$保持不变

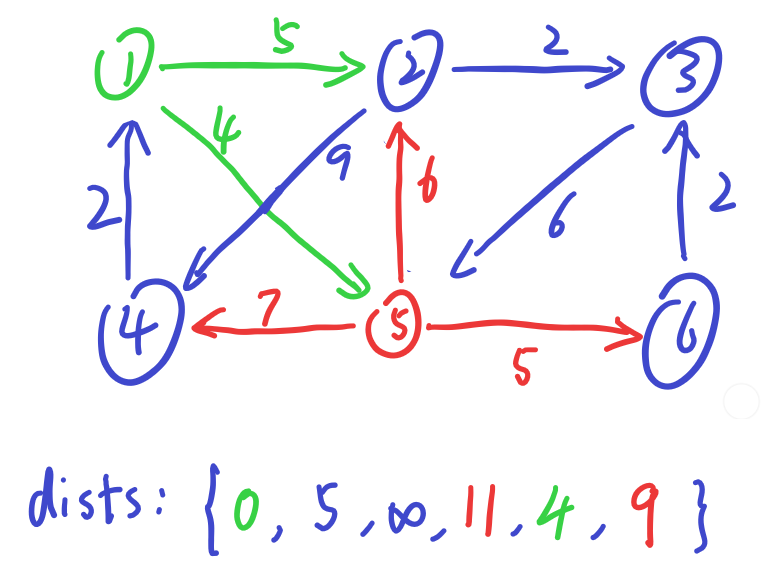
选择节点2，由于6不是2的后继，故$d(6)$不涉及修改

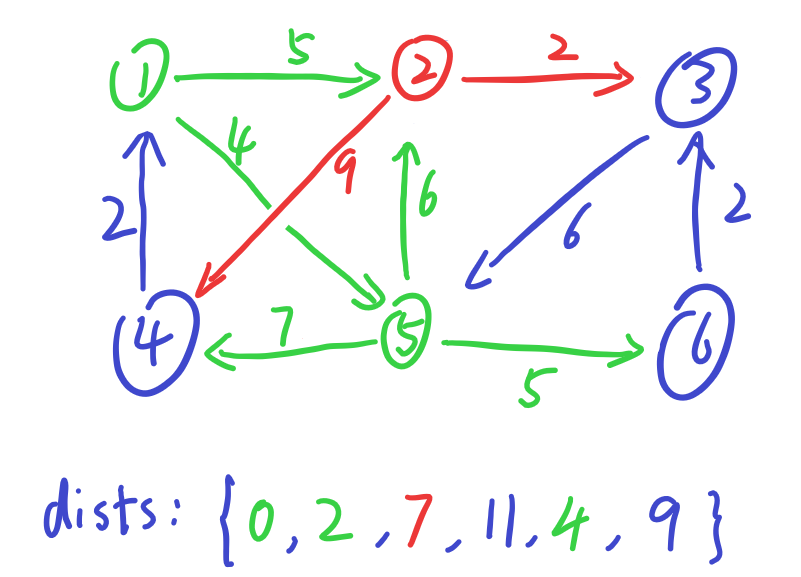
选择节点3，$d(5)$保持不变

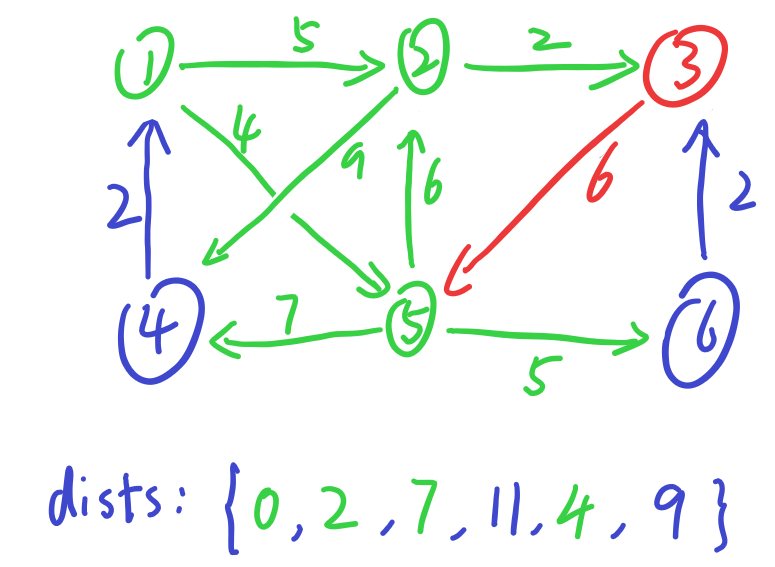
随后依次选择6，4，结果都是不改变任何值，暂时跳过
图可以用邻接矩阵来存储，每一轮找$d(x)$的最小值点，最简单的办法就是枚举每一个$x$并找到最小的$d(x)$，详情请见代码和注释

C++ 代码

以下MGraph类来源于3.0前置知识

vector<int> MGraph::shortestDistance(int s) {   //给定源s，求出它到其余所有节点的最短距离
    //距离表，以及访问表
    vector<int> dists(numVex + 1, 1e9 + 7), visit(numVex + 1, 0);
    dists[s] = 0;//起点距离默认为0
    //一共进行n-1次松弛，n是节点数
    for (int i = 1; i < numVex; i++) {
        int id = 0;
        for (int j = 1; j <= numVex; j++) {
            //从1开始标号的话，0位置的距离就是无穷大了
            if (visit[j] == 0 && dists[id] > dists[j]) {
                //选择未被访问过，且距离更大的节点
                id = j;
            }
        }
        visit[id] = 1;
        //更新后继节点的最短距离（松弛）
        for (int j = 1; j <= numVex; j++) {
            dists[j] = min(dists[j], dists[id] + mat[id][j]);
        }
    }
    return dists;
}