$\Huge\color{orchid}{点击此处获取更多干货}$

拓扑排序

拓扑排序算是BFS的重要衍生，也是考研热点知识
先介绍一下DAG，拓扑序和逆拓扑序：
DAG即有向无环图$\text{(Direct Acyclic Graph)}$，图中的边都是有向的，并且不包含任何回路（环）。拓扑序和逆拓扑序都需要在这样的图结构上产生。
图节点的序列满足拓扑序，指的是对于图中的任意一条边，其起点在节点序列中都排在终点的前面，而逆拓扑序则是反过来，起点都位于终点后面，下图为示例：

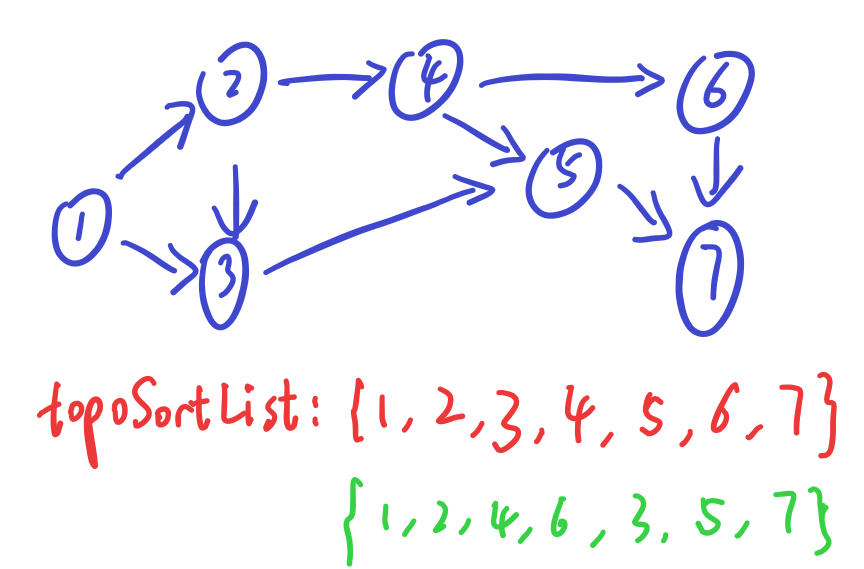
上图中的红色序列即为拓扑序列

求得拓扑序列的方式很简单，就三个关键步骤：
1. 找到所有入度为0的节点
2. 依次遍历（BFS）这些节点，将其所有后继边去掉
3. 重复1，2两步，直到图为空

上述步骤1中，由于0入度节点的遍历顺序不固定，所以拓扑排序可能存在不唯一的结果，上图中，绿色序列也是一条合法的拓扑序列。
另外，如果将所有边反向存储，那么求得的就是逆拓扑序列，之后的代码中只演示拓扑序列，你拓扑序列可以依此类推。

C++ 代码

#pragma GCC optimize(2)
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

//只有有向无环图（DAG）才有拓扑序列
class DAG {
private:
    //拓扑序列，入边表（只需要入度）
    vector<int> topoSortList, inTable, fail = { -1 };
    vector<vector<int>> outTable;//出边表（就是邻接表）
    int numVex, numArc;
    bool isValid = true;//不保证为合法DAG，要判断
public:
    DAG(int n, int m) {
        numVex = n;
        numArc = m;
        //注意从1开始标号
        outTable.resize(n + 1);
        inTable.resize(n + 1);
        int s, e;
        while (m--) {
            cin >> s >> e;
            //根据每对s->e，同时构造出入边表
            outTable[s].push_back(e);
            inTable[e]++;
        }
    }

    //排序后返回拓扑序列
    vector<int>& getTopoSortList() {
        queue<int> q;
        //先加入所有0入度节点
        for (int i = 1; i <= numVex; i++) {
            if (inTable[i] == 0) {
                q.push(i);
            }
        }
        //基于BFS，开始拓扑排序
        while (!q.empty()) {
            //挨个取出0入度节点，并加入拓扑序列
            int cur = q.front();
            q.pop();
            topoSortList.push_back(cur);
            //断开其后继的所有边（所有后继节点入度-1）
            for (auto& nx : outTable[cur]) {
                inTable[nx]--;
                //如果产生了新的0入度节点，继续加入
                if (inTable[nx] == 0) {
                    q.push(nx);
                }
            }
        }
        //当且仅当拓扑序列的长度等于节点数时，拓扑排序才算成功
        if (topoSortList.size() != numVex) {
            return fail;
        }
        else {
            return topoSortList;
        }
    }
};

//输出vector,deque,list,map内元素的<<运算符重载函数
ostream& operator<<(ostream& cout, vector<int> v) {
    for (auto& e : v) {
        cout << e << ' ';
    }
    return cout;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m;
    cin >> n >> m;
    DAG dag(n, m);
    cout << dag.getTopoSortList() << endl;
    return 0;
}