$\Huge\color{orchid}{点击此处获取更多干货}$

BFS

之前遇到的DFS问题，无论是直接在树/图结构中DFS，还是由此衍生出的DFS搜索方法，都有一个自底向上的过程，需要先确保后继节点已经是被访问过的状态，无时空限制的话本问题用DFS也许可以解决，但是很有可能出现下面的情况：

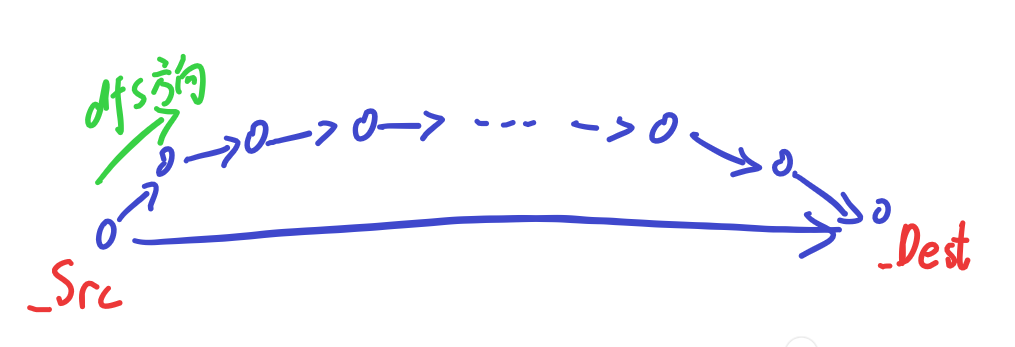
明明从源头到目标只需要走一步，但是DFS由于其“不撞南墙不回头”的特性，得绕远路一直走到目标节点才会回头，这时搜索效率就变得非常低，那么我们换一种方式，同时搜索每一个后继节点，此时绕远路的那一边会进入，但是一步抵达的那一边已经先行查找到了目标，可以不用再管绕远路的那一边，直接报告“目标已找到”

BFS的主要思想就是一轮内访问所有后继，因此对于找“最短距离”“最少步数”之类的特别在行，此后在单源最短路径问题中，还会继续深入介绍，关于BFS算法的细节，可以参考注释

C++ 代码

#pragma GCC optimize(2) 
#include <iostream>
#include <algorithm>
#include <vector>
#include <list>
#include <queue>
using namespace std;

class Graph {
private:
    vector<list<size_t>> adjList;                   //邻接表（无边权，只需要存储节点）
    vector<int> dists;                              //距离表（不用原生指针和数组，可以不调用new/delete）
    constexpr static int _Discon = (int)(1e9 + 7);  //距离无限大代表断连走不通(Disconnected)

public:
    Graph(int n, int m) {
        dists.resize(n + 1, _Discon);
        adjList.resize(n + 1);
        size_t s, e;
        while (m--) {
            cin >> s >> e;
            adjList[s].push_back(e);
        }
    }

    //确定源和目标开始BFS
    int bfs(int _Src, int _Dest) {
        queue<int> q;//用上队列了！
        dists[_Src] = 0;//起点距离为0（之后单源最短路径中也一样）
        q.push(_Src);
        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            //队列中已包含目标节点，就说明找到了，可以直接返回
            if (cur = _Dest) {
                return dists[cur];
            }
            for (auto& nx : adjList[cur]) {
                if(dists[nx] >= _Discon) {  //距离无限大还可以代替vis数组中的false位
                    q.push(nx);
                    dists[nx] = dists[cur] + 1;
                }
            }
        }
        //到这里就说明没找到
        return -1;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m;
    cin >> n >> m;
    Graph G(n, m);
    cout << G.bfs(1, n) << endl;
    return 0;
}