题目描述

给定 $N$ 个正整数 $A_1,A_2,…,A_N$，从中选出若干个数，使它们的和为 $M$，求有多少种选择方案。

输入格式

第一行包含两个整数 $N$ 和 $M$。

第二行包含 $N$ 个整数，表示 $A_1,A_2,…,A_N$。

输出格式

包含一个整数，表示可选方案数。

数据范围

$1 \le N \le 100$,
$1 \le M \le 10000$,
$1 \le A_i \le 1000$,
答案保证在 int 范围内。

输入样例：

4 4
1 1 2 2

输出样例：

3

算法1

(DP，01背包问题) $O(nm)$

我们可以用 01背包问题 解决此问题。

抽象表述：

$a[ \ ]$ $\to$ 物品体积。
$M$ $\to$ 背包容量

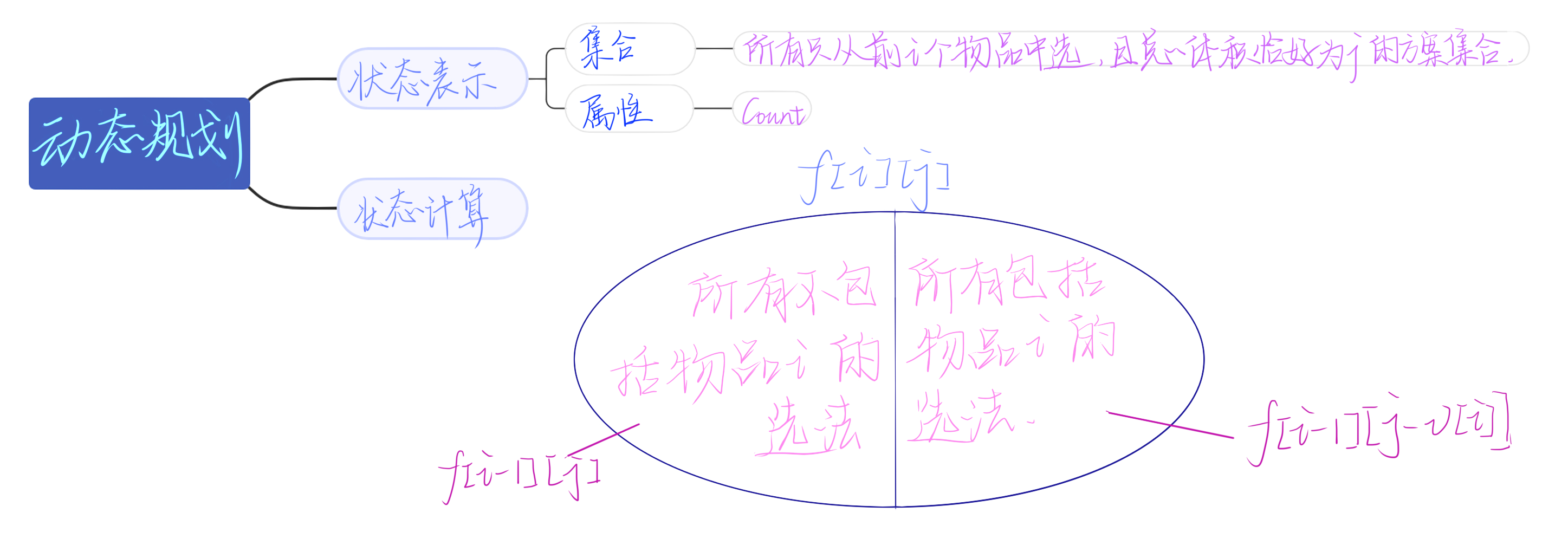
由于此时我们的属性为 $Count$，所以我们对于两种情况的计算方法为 累加，与之前取最大值不同。
也就是此时我们的状态转移方程为：

$$f_{i,j} = f_{i - 1,j} + f_{i,j - a_i}$$

按照之前 AcWing 2. 01背包问题 的方法，我们依然可以通过滚动数组优化掉第一维。
则状态转移方程为：

$$f_{j} = f_{j} + f_{j - a_i}$$
（第 $2$ 个 $f_j$ 为 $f_{i - 1,j}$）

合并简化后为：

$$f_{j} += f_{j - a_i}$$

时间复杂度

参考文献

C++ 代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 110,M = 10010;
int f[M];
int a[N];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i ++) scanf("%d",&a[i]);
    f[0] = 1;
    for(int i = 1;i <= n;i ++){
        for(int j = m;j >= a[i];j --){
            f[j] += f[j - a[i]];
        }
    }
    printf("%d\n",f[m]);
    return 0;
}