$\Huge\color{orchid}{点击此处获取更多干货}$

DFS

深度优先搜索虽然来自于树和图，但并不仅限于此，某些确定目标的搜索问题，中间的搜索状态是相互关联的，可以抽象化为关联式的搜索树，树上每一个节点都是一个状态，这些确定的目标状态一般都位于搜索树的叶子节点处。比如这次的数字排列，以$1 \sim 3$为例，就可以构造出下面的搜索树：

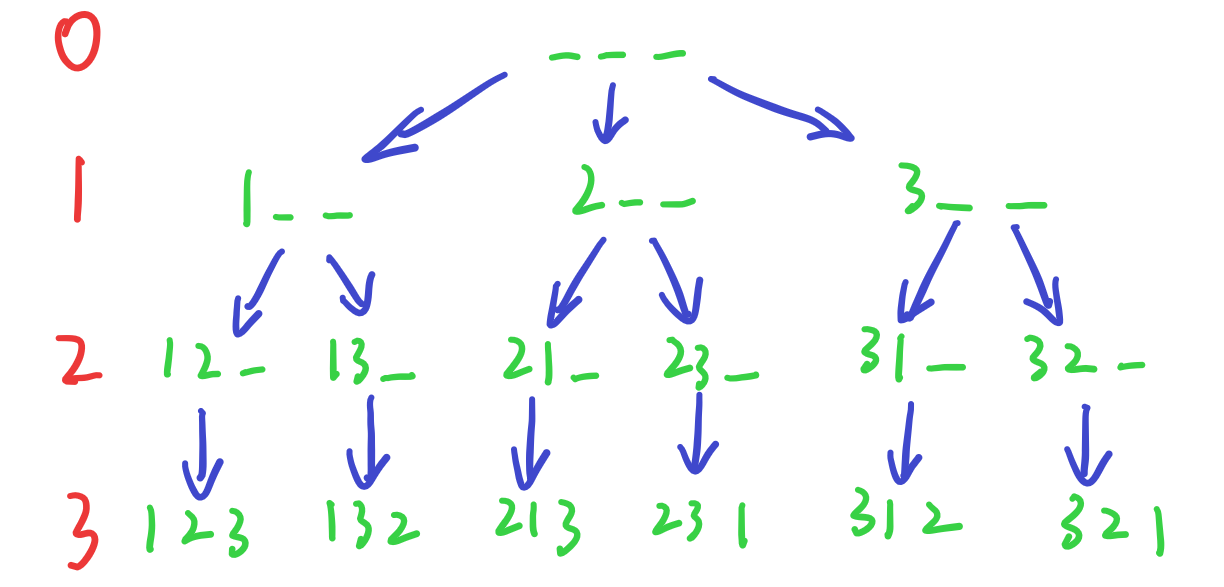
根节点代表所有数都未加入排列的情况，叶子节点作为目标，代表的是所有数字都已经加入排列的情况（这个时候调用输出），每一个中间状态已加入排列的每一个数，在此后续的排列中都不应该再次出现，因此排列的过程中需要记录一下截止到目前有哪些数已经使用过。选择下一个数加入排列的时候，需要在未使用过的数中选择，加入排列之后进入搜索树的更深一层，搜索到目标之后需要回溯。这里回溯操作需要被实际执行，就是取消选择并把加入排列的最后一个数移除

一定有人会觉得，既然DFS需要先递归后回溯，那么树的重心问题中怎么在最后没有把vis[node]改为false呢？问题就在于对节点自身的访问是在后继节点之前还是后继节点之后。上个问题中，需要先统计后继节点的子树大小，然后回到该节点本身，也就是说在统计到某一节点时，其所有后继节点已经能保证被统计过，回溯仅包含一个由系统执行的“函数指针退栈”操作。但是这个问题中，先搜索的是当前节点，然后再进入更深一层。搜索到某节点时，它的某些后继节点还可能处于未访问状态，如果在回退过程中不相应的删除排列的末尾元素，那么搜索到那些未访问的后继节点时，会影响最终结果（大家可以尝试一下，如果把dfs调用的后面两行删除，输出只会留下一行）

C++ 代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;

vector<int> perm;//单次排列
bool* used;//用过的数

int main() {
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    used = new bool[n + 1];//从1开始
    fill(used, used + n + 1, false);
    //参数指的是当前已加入排列的数量，相当于搜索树的层数（从0开始计算）
    function<void(int)> dfs = [&](int cur)->void {
        if (cur == n) { //到达叶子节点
            for(auto& p : perm) {
                cout << p << " ";
            }
            cout << endl;
            return;
        }  
        //在搜索树中先根序搜索
        for (int i = 1; i <= n; i++) {
            //跳过已使用过的数
            if (!used[i]) {
                //加入一个数
                perm.push_back(i);
                used[i] = true;
                dfs(cur + 1);//更深一层
                //回溯时恢复现场（不可或缺）
                used[i] = false;
                perm.pop_back();
            }
        }
    };
    dfs(0);//从0层开始搜索
    delete[] used;
    return 0;
}