$\Huge\color{orchid}{点击此处获取更多干货}$

DFS

对于图结构的三种一般存储方式，深搜和广搜的写法，前述已经备至。邻接矩阵存储法虽然直观清晰，连接两个节点的方式也比较方便，但是存储时需要$O(n^2)$的空间复杂度，遇到节点数比较多，图的稀疏度比较大的情况，会浪费很多存储空间，此时邻接表和链式前向星$O(m)$空间复杂度的优势就体现出来了（该部分使用链式前向星，BFS部分使用邻接表）

之前同样提到过，树是图的特殊情况，而且只有定根、有向的树，用分叉链表存储才不会显得麻烦，问题中限制为了“无向”的树，并且也没有确定根节点，这时用图的存储方式才比较方便，并且由于边数比节点数还少，如果用邻接矩阵存储，这个矩阵的稀疏度将会非常高，因此选用链式前向星存储（邻接表也可）

然后就来关注一下，按照需求描述中“去掉一个节点”，还会剩下哪些部分：

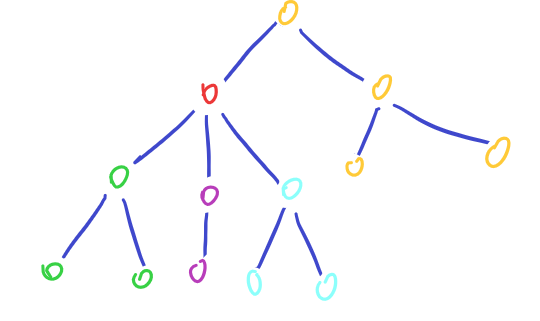
如果去掉了红色节点，那么整个树结构会被分为四部分（分别用四种颜色标记，相同颜色的节点之间相互连通，不同颜色的节点之间互不连通），分别是3个绿色节点，2个紫色节点，3个浅蓝色节点和4个黄色节点，这四部分中节点数最多的部分是黄色部分（共4个节点）。最终的需求是去掉一个节点，使得剩余部分节点数最大值最小。如果把去掉的节点暂时视作根节点，那么去掉它之后，剩余部分节点数的最大值，就在它的各子树节点数，以及整个树结构去掉以它为根的子树之后剩余的节点数之间产生。那么用DFS一次性统计出从根节点开始，以每个节点为根的子树节点数量，然后对于每个节点来说将当前子树中的节点数返回给上一层，这些信息就可以一并得出了。至于根节点如何选择，由于边的无向性，可以任选。细节请见注释（如果不记得链式前向星存储法中，每条数组代表什么，可以回顾一下3.0节前置知识）

最后，一定有人会疑惑，为什么出现了“最小化最大值”需求，却不用二分查找。那是因为二分查找顾名思义，是要“查找”的，并不能保证一次确认成功，而是要反复寻找，判断合理性，这里既然能一次性确认，就不用反复的二分“查找”了

C++ 代码

#include <iostream>
#include <algorithm>
#include <climits>
using namespace std;

int ans = INT_MAX;

class Graph {
private:
    size_t* fin, * last, * pre, tot = 1;
    bool* vis;
    int numVex, numArc;

    //单向连接
    void _connect(size_t s, size_t e) {
        fin[tot] = e;
        pre[tot] = last[s];
        last[s] = tot++;
    }

    //双向连接
    void connect(size_t s, size_t e) {
        _connect(s, e);
        _connect(e, s);
    }
public:
    Graph(int n) {
        numVex = n;
        numArc = 2 * (n - 1);
        fin = new size_t[numArc + 1];
        last = new size_t[numVex + 1];
        pre = new size_t[numArc + 1];
        vis = new bool[numVex + 1];
        fill(last, last + numVex + 1, 0);
        fill(vis, vis + numVex + 1, false);
        size_t s, e;
        for (int i = 1; i < numVex; i++) {
            cin >> s >> e;
            connect(s, e);
        }
    }

    ~Graph() {
        delete[] fin, last, pre, vis;
    }

    int dfs(size_t node) {
        int cur = 0,    //去掉当前节点之后，剩余连通块中节点的最大值
            sum = 1;    //以当前节点为根的子树中，节点的总数
        vis[node] = true;

        //按插入位序，前向访问后继边
        for (size_t i = last[node]; i != 0; i = pre[i]) {
            size_t nx = fin[i];
            if(!vis[nx]) {
                //按后根序，先统计当前节点子树中的节点数量
                int child = dfs(nx);
                cur = max(cur, child);
                sum += child;
            }
        }
        //还要统计除了以它为根的子树之外，剩余节点的数量，并与之比较
        cur = max(cur, numVex - sum);
        ans = min(ans, cur);//最小化cur
        return sum;//返回给上一层累加
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    Graph G(n);
    G.dfs(1);//返回值可忽略
    cout << ans << endl;
    return 0;
}