$\Huge\color{orchid}{点击此处获取更多干货}$

单调队列

单调队列是滑动窗口最值问题的专属数据结构，只要能转化为滑动窗口求最值的模型就可以使用单调队列。
序列上存在一个定长且小于序列长度的滑动窗口，只有窗口内的元素可以被看到，它的头端初始位于序列的头端，每次向后移动时都会遮住最前面的一个元素，然后让后面的元素露出来，这个过程和队列类似，那我们有什么办法，既可以让窗口头端和尾端后面的两个元素按照FIFO的方式增加和删除，又可以在每次滑动后都像普通队列一样在头端取得窗口内的最大值呢？这就是接下来要介绍的单调队列，在这之中做的事情

先来看初始位置，窗口内是$\{1,3,-1\}$，首先我们需要将这三个元素插入队列中，插入1的时候队列是空的，但是插入3的时候队列尾端的1已经比3小了，这时我们需要把1从尾端取出，再把3插入，最后是-1，由于尾端的3已经比-1大了，就可以直接从尾端插入-1。此时头端的3就是最大值

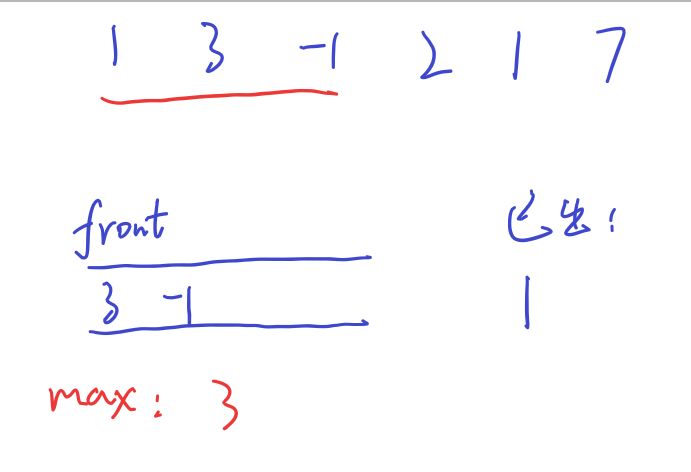
然后，窗口向后移动，之前的1由于已经被3顶掉了最大值之位，不用管它了，加入2之后，尾端-1更小，为了保持头端到尾端的单调减少性，要先从尾端删除-1之后再把2从尾端插入，最大值3不受任何影响

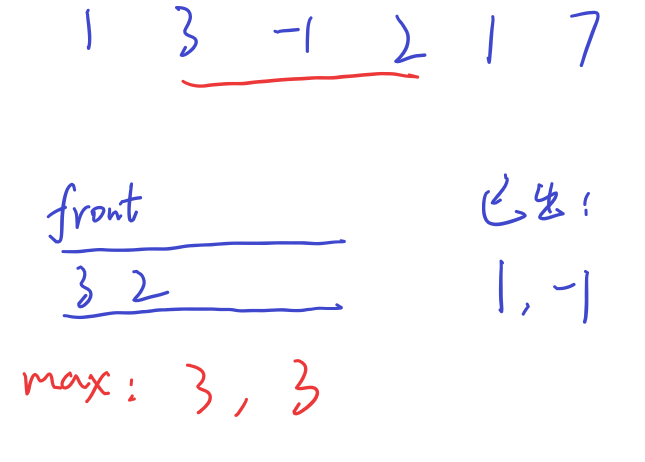
接下来，遮住3，加入1，头端的3由于已经被滑动窗口遮住，不再是最大值候选元素，这时候才是从头端删除，2成为候选元素，由于1比2小，1直接加在尾端

最后的元素7加入时，被遮住的-1不用管，队列里的2和1全都小于7，都要从尾端取出，此时队列已空，直接加入7便可

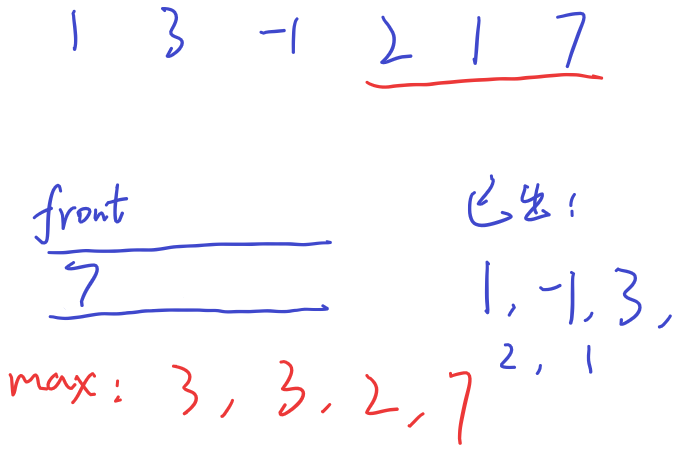
由上述演示过程已经可以看出，插入操作只限定在尾端，但是删除操作既有头端又有尾端，因此STL的queue是满足不了这些需求的，需要利用deque实现一个输入受限的双端队列

C++ 代码

#pragma GCC optimize(2)
#include <iostream>
#include <deque>
using namespace std;

deque<int> ql, qs;//l代表larger，s代表smaller，分别用于求最大，最小值
int* arr, * mx, * mn;//mx代表maximum，mn代表minimum

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, k;
    cin >> n >> k;
    arr = new int[n];
    mx = new int[n];
    mn = new int[n];
    //单调队列里不一定要存放元素值，可以用更通用的方法：存放位序（下标）
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
        //窗口尾端是i，头端是i-k+1，i-k及其左边的位置都需要舍弃
        if (!ql.empty() && ql.front() <= i - k) {
            ql.pop_front();
        }
        if (!qs.empty() && qs.front() <= i - k) {
            qs.pop_front();
        }
        //尾端的元素偏小/大就要出队让位
        while (!ql.empty() && arr[ql.back()] <= arr[i]) {
            ql.pop_back();
        }
        while (!qs.empty() && arr[qs.back()] >= arr[i]) {
            qs.pop_back();
        }
        //最后将当前元素入队
        ql.push_back(i);
        qs.push_back(i);
        //记录最大最小值
        mx[i] = arr[ql.front()];
        mn[i] = arr[qs.front()];
    }
    //从k-1位置开始的最值才有意义
    for (int i = k - 1; i < n; i++) {
        cout << mn[i] << " ";
    }
    cout << endl;
    for (int i = k - 1; i < n; i++) {
        cout << mx[i] << " ";
    }
    cout << endl;
    delete[] arr, mx, mn;
    return 0;
}