$\Huge\color{orchid}{点击此处获取更多干货}$

单调栈

接下来进入栈与队列的第二阶段，这一阶段中内含元素都具备了单调性，这样的栈/队列可以称之为单调栈/单调队列。单调性特征会使这两种特殊结构的应用范围明显缩小，本帖介绍的单调栈，就是查询序列中某元素左/右侧的优先级大于/小于它的第一个元素这类问题的专用数据结构。

下面介绍，对序列中每个元素求其左侧第一个小于它的元素时，需要利用单调栈做些什么：
最重要的一件事，就是确定栈内元素从栈口到栈底，是单调增加还是单调减少。在这个情况下，如果序列元素在准备入栈时，发现栈口的元素比它更小，才说明找到了第一个更小元素，加入当前元素之后，栈口元素比之前的栈口元素更大，因此从栈口到栈底，栈内元素是单调减少的。

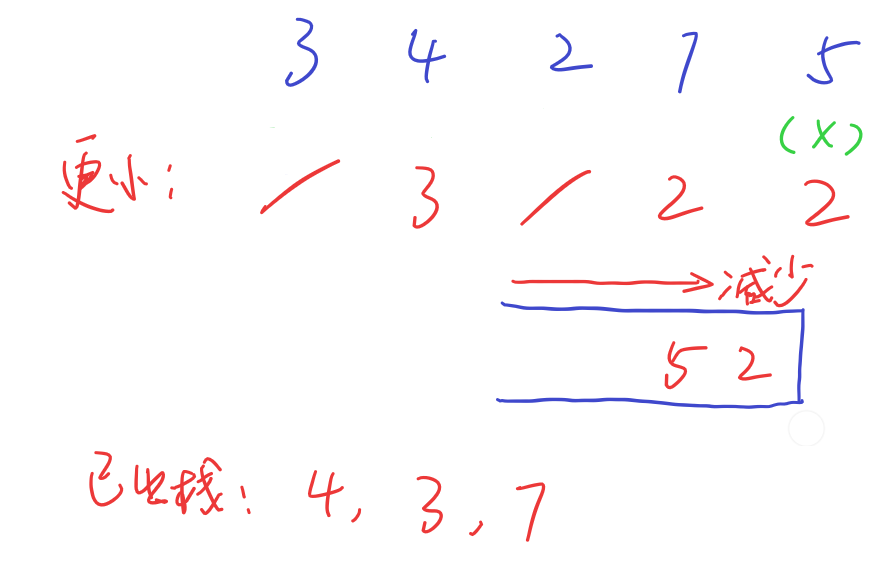
然后，以$\{3,4,2,7,5\}$为例，演示求解过程
初始栈空，3直接入栈，3左侧没有更小元素

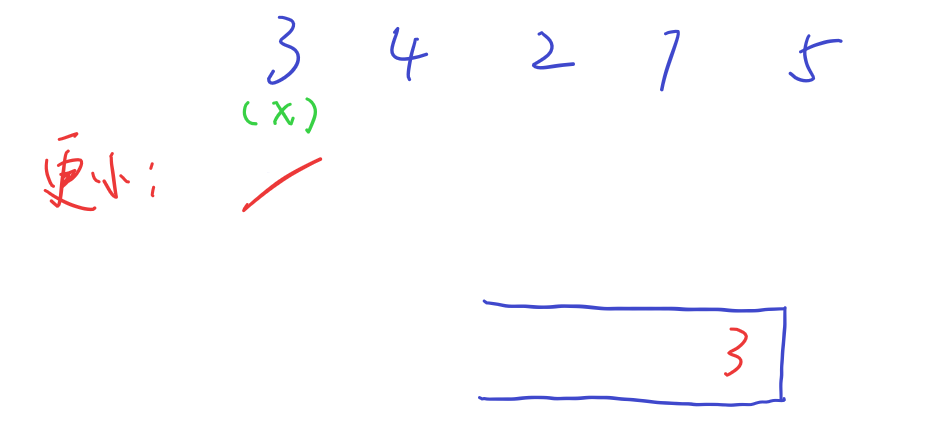
轮到4时，栈口的3比4更小，因此4左侧的第一个更小元素就是3，然后4入栈

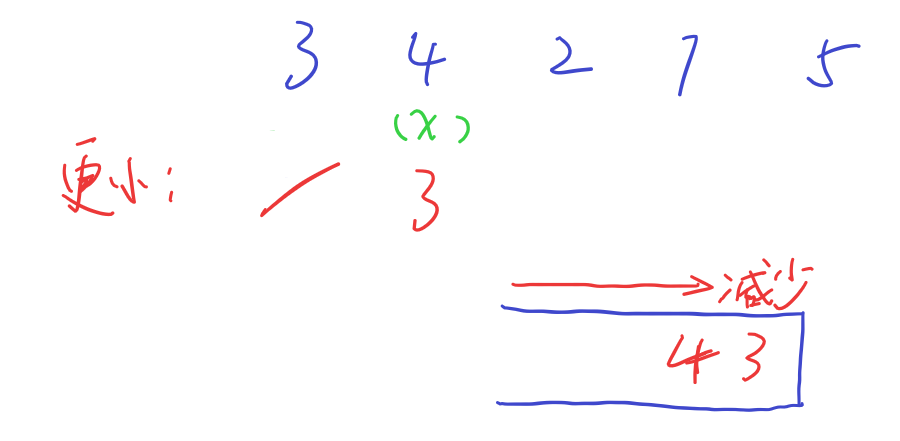
随后，4和3都比2小，直接入2就破坏了单调性，因此4和3都要出栈，栈空了之后才入2

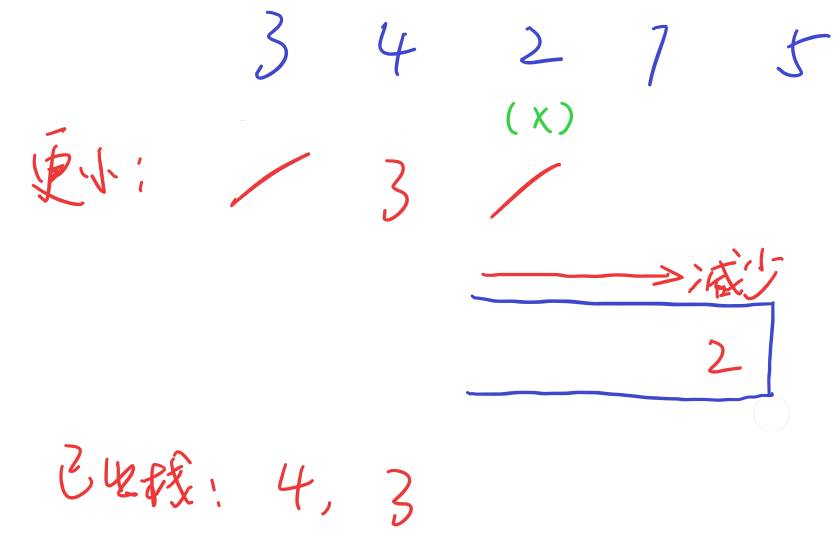
接下来，7准备入栈，栈口已有更小的2，记录之后直接入栈

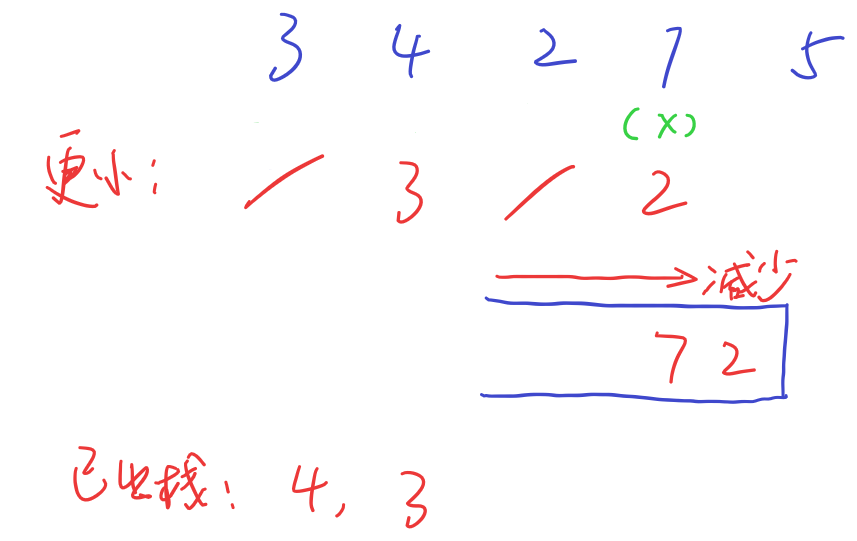
最后是5，栈口7更大，需要出栈，后面的2比5小，记录之后入栈

显然，上述所有入栈、出栈操作，仅用线性表的一端就可完成，直接使用STL的stack

C++ 代码

#include <iostream>
#include <stack>
using namespace std;

stack<int> stk;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        int x; 
        cin >> x;
        //检查单调性，违反单调性的要出栈
        while (!stk.empty() && stk.top() >= x) stk.pop();
        //先输出此时的栈顶元素
        if (!stk.empty()) cout << stk.top() << " ";
        else cout << -1 << " ";
        //输出完成后当前元素才入栈
        stk.push(x);
    }
    return 0;
}