$\Huge\color{orchid}{点击此处获取更多干货}$

双向链表原理

双向链表相比于单向链表，只多了一个前向指针$prev$，因此它可以实现两个方向上的顺序存取，支持的操作也比单向链表多不少，相应的维护链表结构的过程也更复杂。双向链表和单向链表一样，有了头节点也可以更方便的访问链表本身，但是如果跟单向链表一样，只是单纯的反向连接$prev$的话，还是无法克服单向链表对头端以外（尤其是尾端）的节点存取低效的缺点，因此，双向链表的尾端一般需要和头节点也双向连接起来，这样对链表后半段节点的存取效率就有了大大的提升。（STL的list就是这样的双向循环链表结构，在图论部分会用到它）
下图就是双向链表结构的示意图：

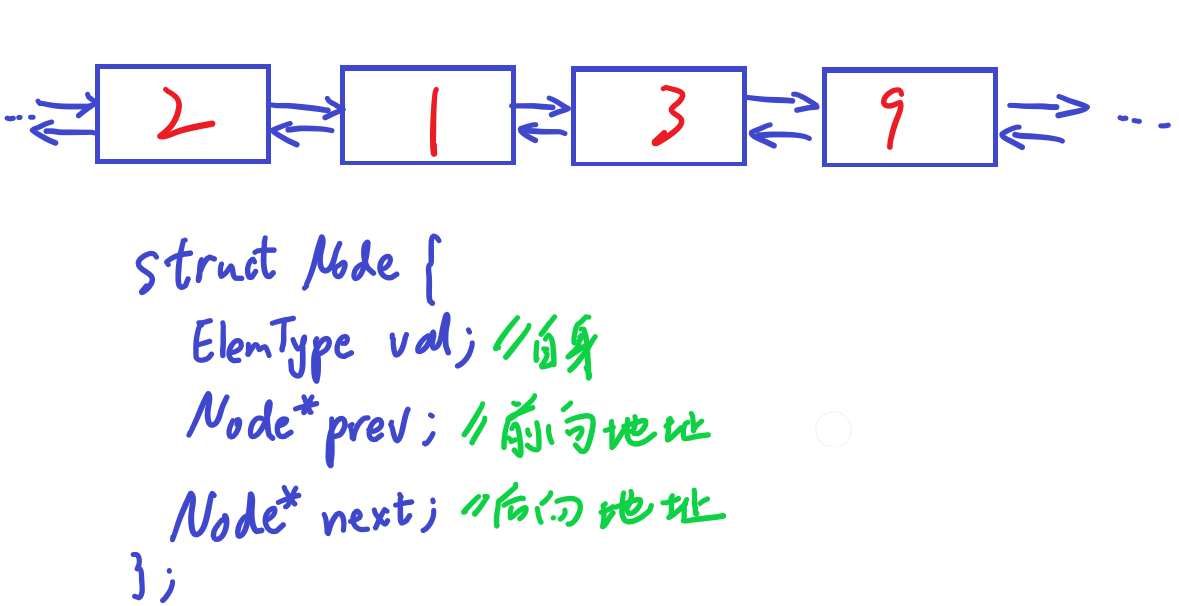
在插入和删除链表节点的时候，跟单向链表类似，只需要修改$prev$和$next$指针即可。由于两个方向上都可以顺序存取，故对于双向链表来说，插入的时候最好同时取得前驱和后继节点。上图中，如果需要在1和3之间插入4，首先需要取得1和3代表的节点$pr$和$nx$，然后构造一个$val=4$的节点，并把该节点的$prev$和$next$分别设置为$pr$和$nx$，最后修改$pr->next$和$nx->prev$，使得新节点位于两者中间，即完成插入

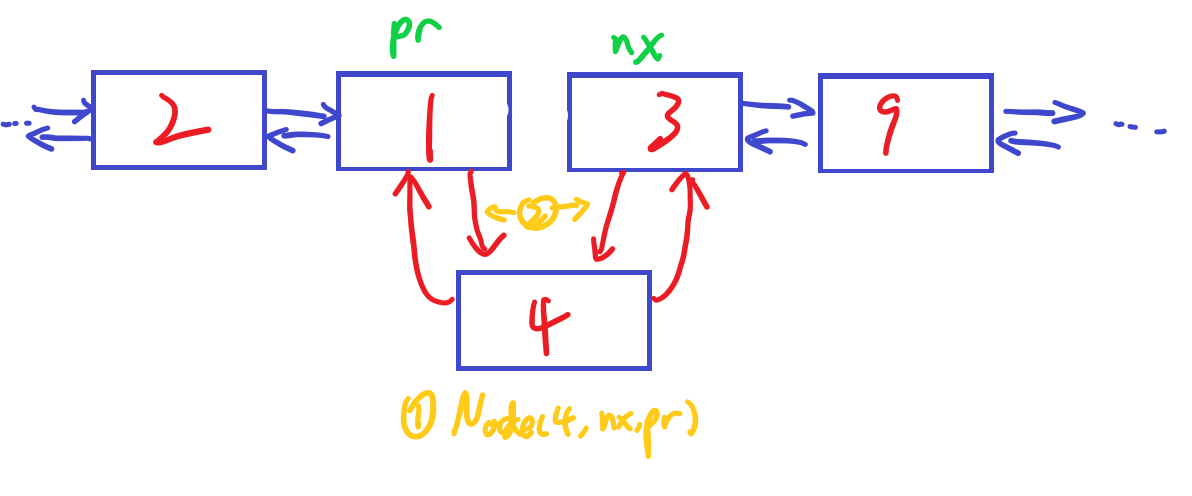
然后，删除元素1时，首先要取得该节点$cur$，然后取得其前驱$pr$和后继$nx$，修改指针使得$pr$和$nx$相邻，最后置空$cur$的两个指针并析构$cur$

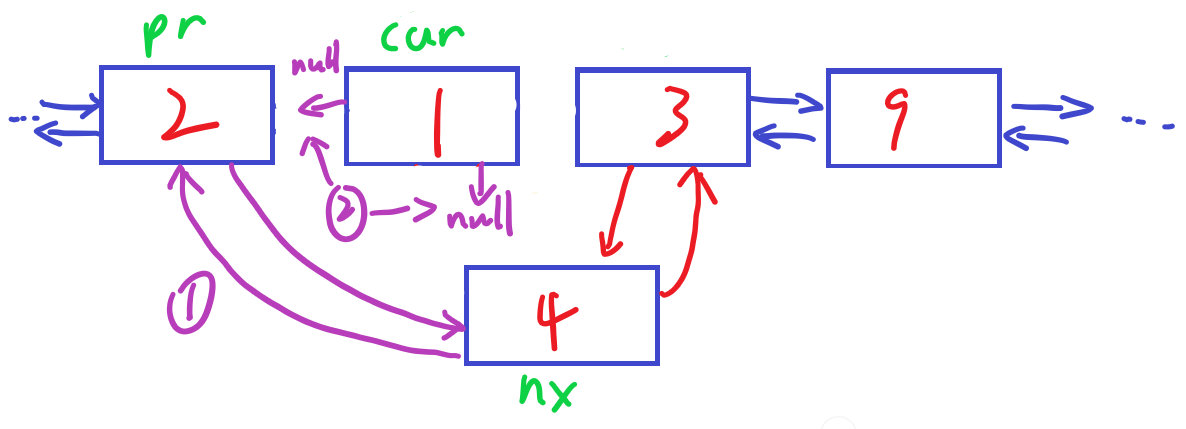
单向链表介绍中提到过，前驱后继指针可以用索引来代替，如果已经提前知道了每个元素的插入位序，其实把插入位序作为索引替代指针也是个不错的选择。这样的链表结构比较接近考研数据结构中定义的“静态链表”，可以方便各位在没有指针也没有引用的编程语言中使用链式结构（但除了汇编语言以外想不到其他的了）

C++ 代码

#pragma GCC optimize(2)
#include <iostream>
#include <vector>
#include <climits>
using namespace std;

//模板参数是可以有默认值的
template<class Elem = int>
struct DLNode {
    Elem val;
    size_t next = ULLONG_MAX, prev = ULLONG_MAX;//size_t上限用来表示空
    DLNode() {}
    DLNode(Elem e) : val(e) {}
    DLNode(Elem e, size_t nxt, size_t pre) : val(e), next(nxt), prev(pre) {}
};

template<class Elem = int>
class DoubleLinkedList {
private:
    //静态链表用索引代替指针，但移除元素后不释放内存
    vector<DLNode<Elem>> existNodes;
    size_t tot = 1, start, finish;
public:
    DoubleLinkedList() {
        //默认有头结点，结构和STL的list一样为双向循环链表
        existNodes.push_back(DLNode(0, 0, 0));
        start = finish = 0;
    }

    //顺序遍历并输出元素
    void traverse() {
        size_t cur = existNodes[start].next;
        while (cur != finish) {
            cout << existNodes[cur].val << " ";
            cur = existNodes[cur].next;
        }
        cout << endl;
    }

    //在第k个节点前插入元素（包含头结点k=0）
    void insertBeforeKthNode(Elem e, size_t k) {
        //插入和取引用不能颠倒，如果插入引起了vector扩容，在此之前取的引用会失效
        existNodes.push_back(DLNode<Elem>(e));
        DLNode<Elem>& nx = existNodes[k], & pr = existNodes[nx.prev];
        existNodes.back().next = k;
        existNodes.back().prev = nx.prev;
        nx.prev = tot;
        pr.next = tot;
        tot++;
    }

    //在第k个节点后插入元素
    void insertAfterKthNode(Elem e, size_t k) {
        existNodes.push_back(DLNode<Elem>(e));
        DLNode<Elem>& pr = existNodes[k], & nx = existNodes[pr.next];
        existNodes.back().next = pr.next;
        existNodes.back().prev = k;
        nx.prev = tot;
        pr.next = tot;
        tot++;
    }

    //开头或末尾插入元素，只要调用k=0的插入函数即可
    void insertAtFirst(Elem e) {
        insertAfterKthNode(e, 0);
    }

    void insertAtEnd(Elem e) {
        insertBeforeKthNode(e, 0);
    }

    //删除元素
    void eraseKthNode(size_t k) {
        DLNode<Elem>& cur = existNodes[k], 
            & pr = existNodes[cur.prev], 
            & nx = existNodes[cur.next];
        pr.next = cur.next;
        nx.prev = cur.prev;
        cur.next = cur.prev = ULLONG_MAX;
    }
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    string op;
    size_t k;
    int x, n;
    cin >> n;
    DoubleLinkedList list;
    while (n--) {
        cin >> op;
        if (op == "L") {
            cin >> x;
            list.insertAtFirst(x);
        }
        else if (op == "R") {
            cin >> x;
            list.insertAtEnd(x);
        }
        else if (op == "D") {
            cin >> k;
            list.eraseKthNode(k);
        }
        else if (op == "IL") {
            cin >> k >> x;
            list.insertBeforeKthNode(x, k);
        }
        else if (op == "IR") {
            cin >> k >> x;
            list.insertAfterKthNode(x, k);
        }
    }
    list.traverse();
    return 0;
}