$\Huge\color{orchid}{点击此处获取更多干货}$

有序离散化

问题的需求已经见过了，但是这次的序列并没有定长，而且也不是连续的序列，先看一下可能出现的情况：

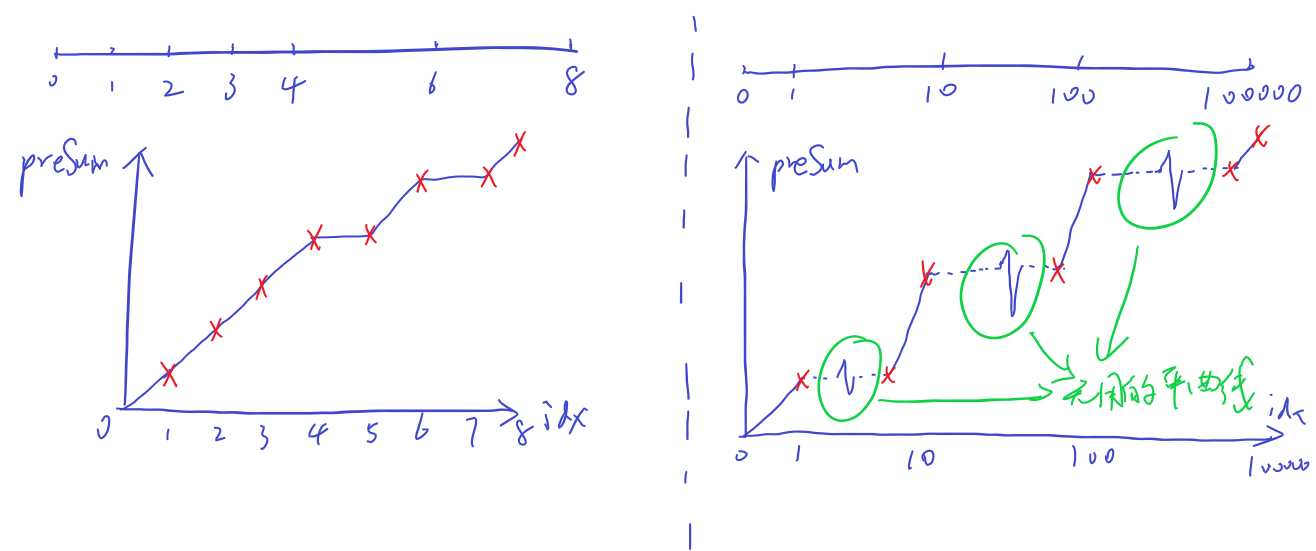
左边的连续程度相对较高，前缀和的增量曲线还是比较平滑的，但是右边的就属于这次的问题可能出现的情况，明明只有很少的有效元素，但是它们散列在了10万长度的范围内，在这种情况下用连续序列的前缀和求解方式，前缀和增量曲线将会有很大一部分是毫无作用的水平线，也极大的浪费了计算时间和存储空间。这种情况下，就不再适合用完全连续的序列存储了，而是要将序列看成若干离散的元素来存储，类似于稀疏矩阵完全离散的COO存储格式（如下图）

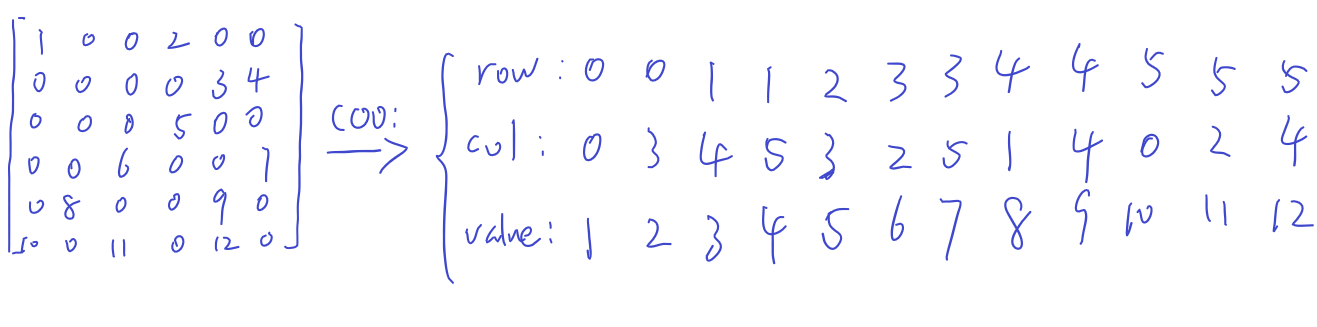
同样，为了方便计算，和COO格式存储的矩阵一样，需要保证有效元素位置的相对有序，因此还需要对预先离散化后的有效位置进行排序，必要时还得去重（如上图中的COO格式，为了方便存取一行，让有效元素位置按照行优先的方式排了序）

回到问题本身，再来看一个例子：

超过10万的长度上，真正起作用的只有14（去重之后11个位置），为了保持其相对有序性，所有的有效位置需要升序排列，去除重复元素，然后才能用连续的线性表存储并求得前缀和。可以见得，离散化后，前缀和增量曲线上无用的水平线长度明显减少了很多。范围查询时，由于有效位置已经升序，故可以用二分查找（STL中有$lower\_bound$函数，能找到不小于某个元素的首个位置），取得离散化后的两端点，然后按照一元前缀和的方法取得段内元素和，细节请见注释

C++ 代码

#pragma GCC optimize(2)
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

vector<int> positions;//所有出现过的位置
vector<pair<int, int>> commands, range;//修改指令集和查询范围集

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m;
    cin >> n >> m;
    int x, c;
    for (int i = 0; i < n; i++) {
        cin >> x >> c;
        positions.push_back(x);
        commands.push_back({ x, c });
    }
    int l, r;
    for (int i = 0; i < m; i++) {
        cin >> l >> r;
        positions.push_back(l);
        positions.push_back(r);
        range.push_back({ l, r });
    }
    //排序去重（用不上哈希表，因为用上了一样要排序，但是哈希表类不带sort成员函数）
    sort(positions.begin(), positions.end());
    positions.erase(
        //unique的作用是将所有重复元素移到序列末尾，并返回无重复元素部分的末尾迭代器
        unique(positions.begin(), positions.end()), 
        positions.end()
    );
    int len = positions.size();
    //offset是离散化后每个有效位置上的偏移量，preSum是offset的前缀和
    int* preSum = new int[len + 1], *offset = new int[len + 1];
    *preSum = 0;
    fill(offset, offset + len + 1, 0);//不填充0，加法会出问题
    //二分查找离散化之后的位置
    auto newPos = [=](int pos)->int {
        //positions表从0开始记录，而offset表从1开始记录，需要对齐
        return lower_bound(positions.begin(), positions.end(), pos) - positions.begin() + 1;
    };
    for (auto& [pos, ofs] : commands) {
        int p = newPos(pos);
        offset[p] += ofs;
    }
    //求离散化的前缀和
    for (int i = 1; i <= len; i++) {
        preSum[i] = preSum[i - 1] + offset[i];
    }
    for (auto& [l, r] : range) {
        int left = newPos(l), right = newPos(r);
        cout << preSum[right] - preSum[left - 1] << endl;
    }
    //delete[]整个就是运算符，可以在后面连着跟上用过new[]的指针
    delete[] offset, preSum;
    return 0;
}

离散化方法在计算机科研中算是比较常见的，我正在研究的稀疏矩阵相乘（SpMM）算法就需要离散化存储稀疏矩阵，以及算法领域中的朴素贝叶斯分类算法，也是基于离散数据集的，学会离散化大有益处