$\Huge\color{orchid}{点击此处获取更多干货}$

多元差分

考研数学中的差分方程只有一元，暂未找到多元差分方程的定义，但是可以留意一下函数微分：
$$df(x) = f’(x)dx = \lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} dx（一元）$$
$$df(x,y)=f’_xdx+f’_ydy=\lim_{\Delta x \to 0} \frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}dx+\lim_{\Delta y \to 0} \frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}dy（多元）$$

如果把上述$\Delta x,\Delta y$全部视作1，那么也可以类比的给出差分定义：
$$\Delta f(x) = f(x+1)-f(x)（一元）$$
$$\Delta f(x,y) = f(x+1,y+1)-f(x,y+1)-f(x+1,y)+f(x,y)（多元）$$

接下来再来关注一下，对矩阵某一区域执行整体偏移，差分值发生了怎样的变化：

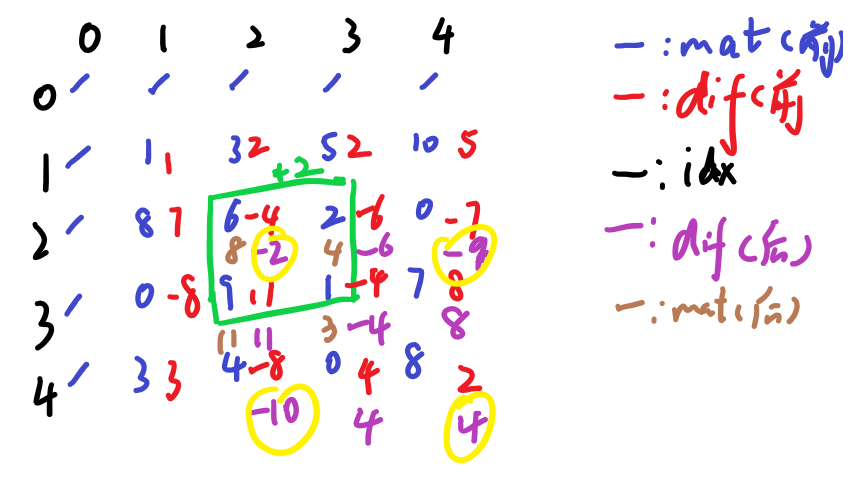
偏移量$c=2$，区域左上角和右下角元素的右下方，差分值增加了$c$，右上角右方和左下角下方，差分值减少了$c$。其余偏移指令可以在此差分矩阵上修改对应值来执行，最后对差分矩阵求多元前缀和，就可以得到最终的矩阵

C++ 代码

#include <iostream>
#include <algorithm>
using namespace std;

int** mat, ** dif;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m, q;
    cin >> n >> m >> q;
    mat = new int* [n + 2];
    dif = new int* [n + 2];
    for (int i = 0; i <= n + 1; i++) {
        mat[i] = new int[m + 2];
        dif[i] = new int[m + 2];
        //周围一圈都留一位，左方和上方有意义，必须赋值0
        fill(mat[i], mat[i] + m + 2, 0);
        fill(dif[i], dif[i] + m + 2, 0);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> mat[i][j];
            //根据类比定义得出每个差分值
            dif[i][j] = mat[i][j] - mat[i - 1][j] - mat[i][j - 1] + mat[i - 1][j - 1];
        }
    }
    int x1, x2, y1, y2, c;
    while (q--) {
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        //根据示意图修改对应值
        dif[x1][y1] += c;
        dif[x2 + 1][y1] -= c;
        dif[x1][y2 + 1] -= c;
        dif[x2 + 1][y2 + 1] += c;
    }
    //求多元前缀和
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            dif[i][j] += (dif[i - 1][j] + dif[i][j - 1] - dif[i - 1][j - 1]);
            cout << dif[i][j] << " ";
        }
        cout << endl;
    }
    for (int i = 0; i <= n + 1; i++) {
        delete[] mat[i], dif[i];
    }
    delete[] mat, dif;
    return 0;
}