$\Huge\color{orchid}{点击此处获取更多干货}$

差分

差分在考研数学的高等数学部分，出现了明确定义的差分方程：
$\Delta y=y(t+1)-y(t)（一阶差分）,$
$\Delta ^2 y = \Delta (\Delta y) = y(t+2)-y(t+1)-(y(t+1)-y(t))=y(t+2)-2*y(t+1)+y(t)（二阶差分）,$
$…$
其中正包含了“差分”的明确定义：函数值在长度为1的区间上的增量
对于序列来说，序列上的差分正是某一位置上的元素与其前一位元素的差值

接下来关注一下，给予序列中某一区段一定量的偏移之后，序列中的差分值发生了什么样的变化：

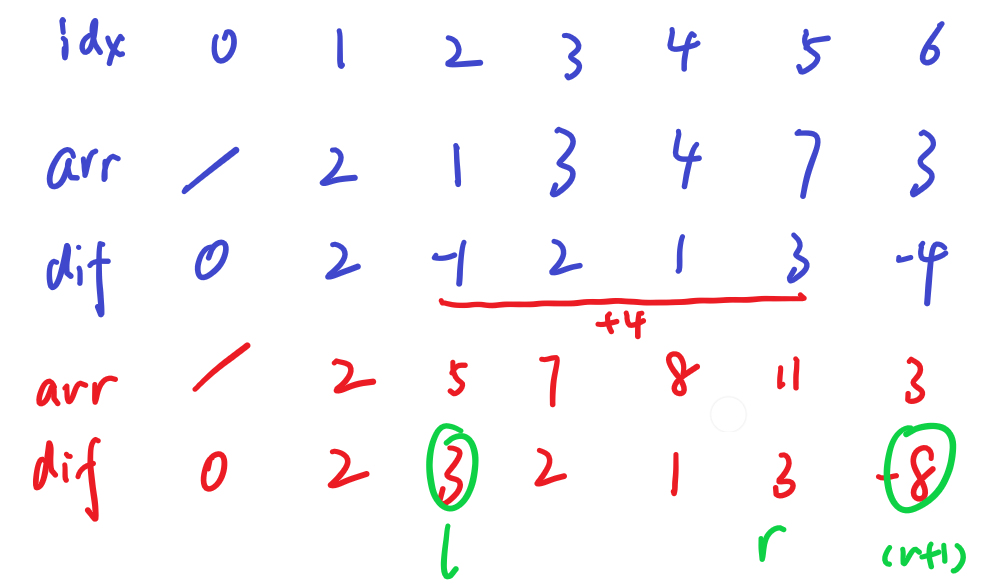
由图可知，在偏移量$c=4$的影响下，段首的差分值增加了$c$，段内其余位置不变，但是段尾后面一位的差分值相应的减少了$c$。在此基础上进行其他区段的整体偏移，也只需要继续修改新的差分值即可。执行完所有偏移之后，只要再对差分序列求前缀和，就可以还原为偏移执行完毕之后的序列

但是，差分序列只能用于一次性的处理完所有偏移指令，随后才能还原，如果是偏移和还原交错进行，就不是单独一个差分序列能高效解决的问题了，这个问题会在提高篇中遇到

C++ 代码

#include <iostream>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    //x是当前值，last是上一位的值
    int n, m, x, last = 0;
    cin >> n >> m;
    //两端都留一位，减少边界讨论
    int* dif = new int[n + 2];
    dif[0] = 0;//头端留的这一位是有意义的
    for (int i = 1; i <= n; i++) {
        cin >> x;
        //按照定义给每一位赋值
        dif[i] = x - last;
        last = x;
    }
    int l, r, c;
    while (m--) {
        cin >> l >> r >> c;
        //此区段整体偏移的时候，只有两端的差分值发生了变化
        dif[l] += c;
        dif[r + 1] -= c;
    }
    //差分序列上求前缀和，可以得到原序列
    for (int i = 1; i <= n; i++) {
        dif[i] += dif[i - 1];
        cout << dif[i] << " ";
    }
    cout << endl;
    delete[] dif;
    return 0;
}