$\Huge\color{orchid}{点击此处获取更多干货}$

二分查找

这是整数型二分查找的模板问题，考研中主要以填选的形式出现，但频率也较高，最常用到的场合就是在有序序列中，但不仅限于有序序列，之后将从另一个角度来介绍
二分查找也是一种分治算法，通过不断地取中点缩小查找范围，最终查找到目标值。取中点可以向上取整也可以向下取整，关于何时向哪个方向取整，下面的两张图能给出解答：

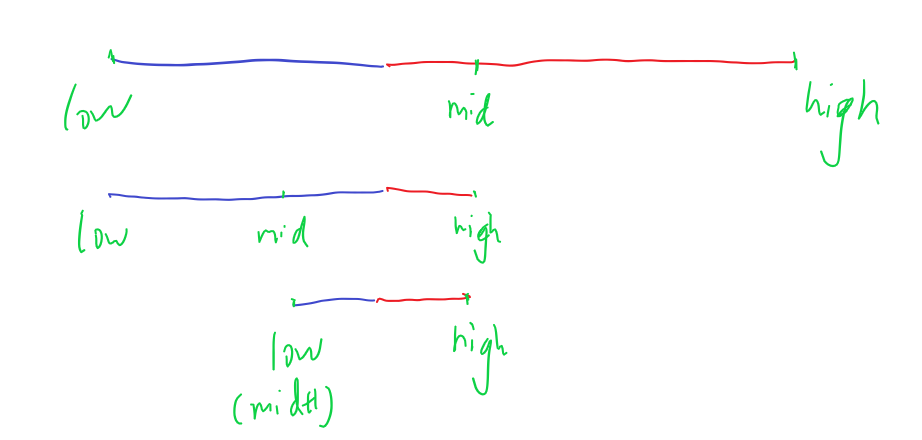
第一张图中，红色位于序列右半区，其一端点固定为序列右侧端点，如果需要查找红色区域的另一端点，就需要在取中点的时候向下取整，如果中点$mid$是红色，那么从$mid+1$到$high$这一段全都是红色，不可能存在红色区域的待查端点，此时需要把$high$移动到$mid$的位置（第一次查找）；第二次查找，$mid$为蓝色，那么从$low$到$mid$区域内一定都是蓝色，这时就需要把$low$移动到$mid+1$的位置。以此类推，直到$low$和$high$相遇，相遇位置就是红色区域的另一端点
向下取整的模板为：

int low = 0, high = len - 1;
while (low < high) {
    int mid = (low + high) / 2;
    if (check(mid)) {
        high = mid;
    }
    else {
        low = mid + 1;
    }
}

其中check函数可以用普通函数或lambda表达式定义，也可以用一个布尔表达式直接代替

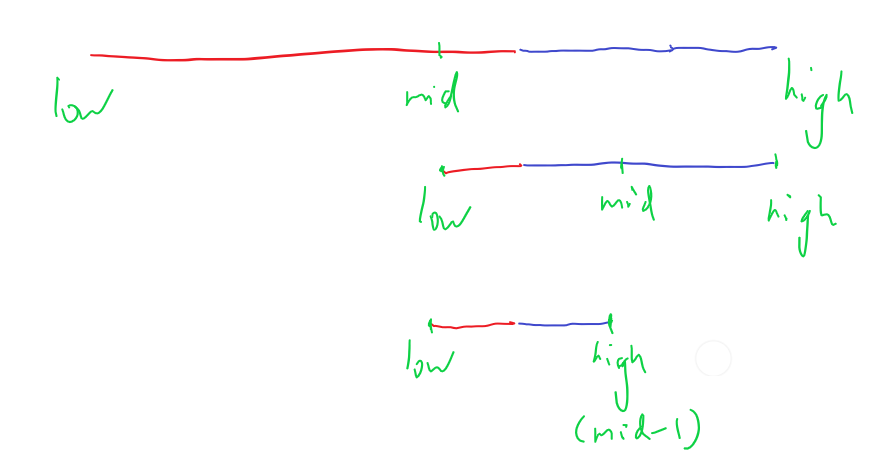
第二张图，红色位于左半区，和第一张图大同小异，至于这里为什么要向上取整，假设到最后一步$low+1=high$，$low$是红色而$high$是蓝色，那么向下取整时$mid$取$low$，发现是红色之后$low=mid$，实际上$low$压根没动，这样就死循环了，而向上取整之后$mid$取$high$，发现是蓝色之后，$high$移动到$mid-1$也就是$low$的位置，此时循环结束，端点查找成功
向上取整的模板为：

int low = 0, high = len - 1;
while (low < high) {
    int mid = (low + high + 1) / 2;
    if (check(mid)) {
        low = mid;
    }
    else {
        high = mid - 1;
    }
}

实际问题中，线段的红和蓝就相当于布尔值true和false，在使用二分查找的时候就可以把check函数的值(true和false)视作红线段和蓝线段，除此之外还需要确定三件事：如何区分红与蓝，红蓝分布是否二元化，以及红线段偏向哪一侧。详情请见注释

C++ 代码

#include <iostream>
#include <algorithm>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, q;
    cin >> n >> q;
    int* arr = new int[n];
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }
    int k, low, high;
    //可以用>=和<=两种关系夹逼出来
    while (q--) {
        cin >> k;
        //先查找不小于k的左端点
        //对于arr[id] >= k的条件来说，红线段位于右侧
        low = 0;
        high = n - 1;
        while (low < high) {
            int mid = (low + high) / 2;
            if (arr[mid] >= k) {    //check函数就用bool表达式arr[mid] >= k代替了
                high = mid;
            }
            else {
                low = mid + 1;
            }
        }
        //这里是有可能查找失败的，循环结束后本该成为红线段左端点的low位置如果元素值不等于k，那就直接判断失败
        if (arr[low] != k) {
            cout << "-1 -1" << endl;
        }
        else {
            cout << low << " ";
            //确定了不小于k的左端点之后，继续在剩下的序列中查找不大于k的右端点
            //对于arr[id] <= k的条件来说，红线段位于左侧
            high = n - 1;
            while (low < high) {
                int mid = (low + high + 1) / 2;
                if (arr[mid] <= k) {
                    low = mid;
                }
                else {
                    high = mid - 1;
                }
            }
            //此时就不用判断查找失败了
            //因为如果在>=条件下成功查找到了等于k的元素并且它位于low位置
            //那么剩下部分中的high最少也会停留在low处，arr[high]一定是等于k的
            cout << high << endl;
        }
    }
    delete[] arr;
    return 0;
}