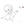2024寒假每日一题全部题解传送门>>

根据题意，对于$i>1$总是有$p_i-p_{i-1}\geq2$的意思就是保证子序列中的每个字符在原字符串中对应的位置两两不相邻，换句话说，选取了第$i$个位置的字符后，就不能选取第$i+1$和第$i-1$个位置的字符。所以对于原字符串中的每个字符，都有选和不选两种选择，故考虑用$dp$来做。根据闫氏$dp$分析法，用$f[i][0]$和$f[i][1]$分别表示不选第$i$个位置字符和选取第$i$个位置字符对应的最大价值。现在对这两种情况进行讨论：
1. 不选第$i$个位置的字符：
那么此时可以选第$i-1$个位置的字符和不选第$i-1$个位置的字符：
（1）选取第$i-1$个位置的字符：即$f[i][0]=f[i-1][1]$。
（2）不选取第$i-1$个位置的字符：即$f[i][0]=f[i-1][0]$。
故$f[i][0]=max(f[i-1][0],f[i-1][1])$。
2. 选取第$i$个位置的字符：
那么此时不能选第$i-1$个位置的字符了，即：
$f[i][1]=f[i-1][0]+$该位置字符对应的价值。

那么最终答案即为$max(f[n][0],f[n][1])$。

C++代码：

#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e6 + 10;
char str[N];
int f[N][2];

int main()
{
    scanf("%s", str + 1);

    int n = strlen(str + 1);

    f[1][1] = str[1] - 'a' + 1;   
    for(int i = 2; i <= n; i ++)
    {
        f[i][0] = max(f[i - 1][0], f[i - 1][1]); // 不选
        f[i][1] = f[i - 1][0] + str[i] - 'a' + 1; // 选
    }

    printf("%d", max(f[n][0], f[n][1]));
    return 0;
}