AcWing 3417. 砝码称重(闫式dp/dfs)

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 3417. 砝码称重(闫式dp/dfs) 原题链接简单

作者：

数学汤家凤 , 2021-04-28 19:32:59 , 所有人可见 , 阅读 12311

138

45

题目描述

你有一架天平和 N 个砝码，这 N 个砝码重量依次是 W1,W2,⋅⋅⋅,WN。

请你计算一共可以称出多少种不同的正整数重量？

注意砝码可以放在天平两边。

算法1

(dp) $O(nm)$

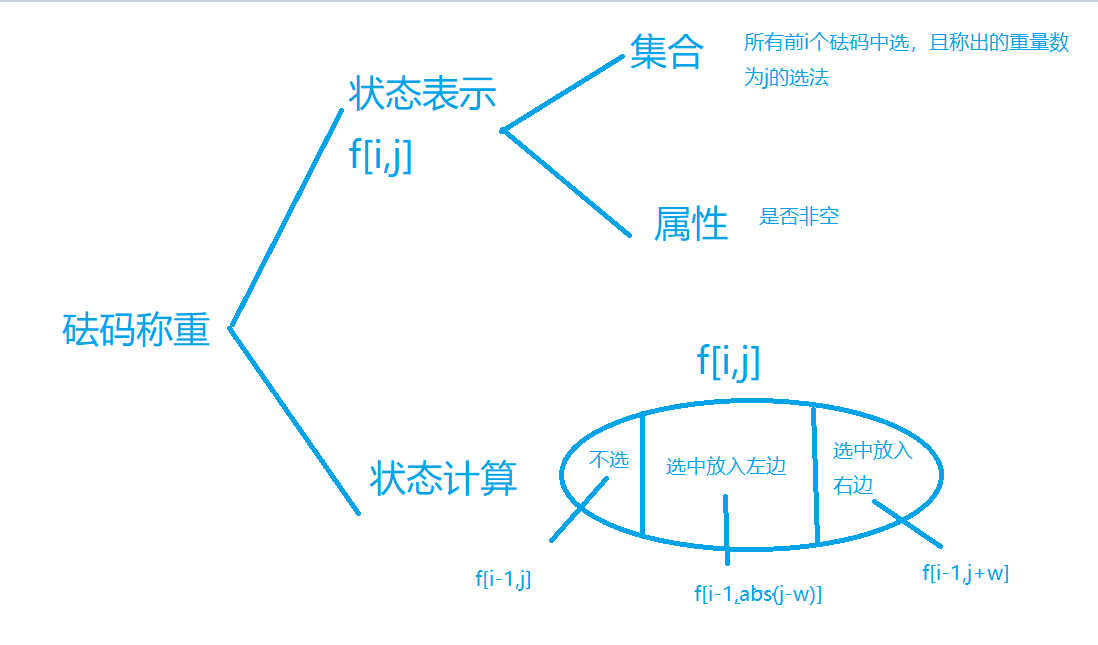
由实际含义可以，f[i][j]=f[i][-j] 因为可以通过镜像的操作而得到，故而f[i][j-w]=f[i][w-j]=f[i][abs(j-w)]。就避免了数组下标为负数的情况

C++ 代码

#include <bits/stdc++.h>

using namespace std;

const int N = 110, M = 2e5 + 10;
int sum;
int n;
int w[N];
bool f[N][M];

int main() {

    cin>>n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &w[i]);
        sum+=w[i];
    }

    f[0][0]=true;

    for (int i = 1; i <= n;i++)
        for (int j = 0; j <=sum;j++)
            f[i][j]=f[i-1][j]||f[i-1][j+w[i]]||f[i-1][abs(j-w[i])];
                //只要有一个非空,f[i][j]就非空
    int ans = 0;
    for (int i = 1; i <=sum;i++)
        if(f[n][i])ans++;//不为零说明可以选出这个质量的砝码

    cout << ans;

    return 0;
}

算法2

(暴力枚举过一半的数据)

C++ 代码

#include<stdio.h> 
int n;
int res;
int w[1000000]; 
bool st[100000];
void dfs(int k,int sum)//表示k个的砝码,重量是sum 
{
    if(k>n)//k>n 说明选完n个砝码 
    {
        if(sum>0&&!st[sum])// 判断选出来的n个砝码的重量是否没被标记过 ，如没标记则答案加1 
        {
            res++;
            st[sum]=true;//标记这个重量 
            return;
        }   
    }
    //还没选够n个砝码 
    else
    {
        dfs(k+1,sum-w[k]);//砝码放右边 
        dfs(k+1,sum);//跳过，不选用当前的砝码 
        dfs(k+1,sum+w[k]);//砝码放左边 
    }
}
int main()
{
    scanf("%d",&n); 
    for(int i=1;i<=n;i++)scanf("%d",&w[i]); 

    dfs(0,0);
    printf("%d",res); 
}

95 评论

lianyh不是dd 2023-04-03 16:29

汤神，我高数跟定你啦

外乡人 7个月前

真是清清又爽爽啊

无限前进 2023-04-04 11:48

求大佬解释一下为什么这里的数组还需要开两倍啊？

7suki 2023-04-05 16:44

我也想知道这里为什么只有开两倍才能过, 这里abs不是没有偏移量嘛

Catw1thu 2023-04-06 00:31 回复了 7suki 的评论

我觉得如果数据只有一个砝码，重量是1e5，那么当j=1e5，转移时的f[i][j+w[i]]就越界了，所以开了两倍。

7suki 2023-04-06 07:40 回复了 Catw1thu 的评论

清晰了!!!

无限前进 2023-04-06 10:15 回复了 Catw1thu 的评论

原来如此，感谢大佬

TaTaTa110 8个月前

可以不开两倍

#include <bits/stdc++.h>

using namespace std;

const int N = 110, M = 1e5 + 10;
int sum;
int n;
int w[N];
bool f[N][M];

int main() {

    cin>>n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &w[i]);
        sum+=w[i];
    }

    f[0][0]=true;

    for (int i = 1; i <= n;i++)
        for (int j = 0; j <=sum;j++)
        {    
            f[i][j]=f[i-1][j]||f[i-1][abs(j-w[i])];
            if (j + w[i] <= sum) f[i][j] |= f[i - 1][j + w[i]];
        }    
                //只要有一个非空,f[i][j]就非空
    int ans = 0;
    for (int i = 1; i <=sum;i++)
        if(f[n][i])ans++;//不为零说明可以选出这个质量的砝码

    cout << ans;

    return 0;
}

只要判断一下数组别越界就行

风起于浮萍之末 7个月前回复了 Catw1thu 的评论

可是说的是总重

cc_25 7个月前回复了 Catw1thu 的评论

%%%

颓废 2023-03-27 20:30

orz

浪浪_ 7个月前

####bfs过四个
####为什么dfs可以过五个！！！

import java.io.*;
import java.util.*;

public class Main{
    public static void main(String[] args) throws Exception {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(in.readLine().trim());

        String[] s0 = in.readLine().split("\\s+");
        int[] h = new int[110];
        for(int i = 0;i<n;i++)
        {
            h[i] = Integer.parseInt(s0[i]);
        }
        boolean[] use = new boolean[100010];

        long res = 0;
        Queue<int[]> q = new LinkedList<>();
        q.add(new int[]{0,0}); // 次数 + 重量
        while(!q.isEmpty())
        {
            int[] a = q.poll();
            if(a[0]>n)  
            {
                if(a[1]>0 && !use[a[1]])
                {
                    res++;
                    use[a[1]] = true;
                }
            }
            else
            {
                q.add(new int[]{a[0]+1,a[1]-h[a[0]]});
                q.add(new int[]{a[0]+1,a[1]});
                q.add(new int[]{a[0]+1,a[1]+h[a[0]]});
            }

        }
        out.println(res);
        out.flush();
    }
}