中国剩余定理

作用:求n组线性同余方程的通解
使用前提:$对于\forall i \in [1,n],x \equiv m_i(mod \quad a_i) ,其中若m_1,m_2,\ldots,m_n \color{Red}{两两互质},则可以使用中国剩余定理来求解x$
形式: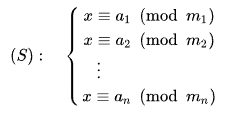
公式: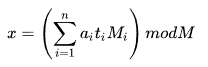
$其 中t_i 是 M_i 的逆元,M_i=M/m_i(除了m_i以外的乘积),M=m_1\*m_2\*m_3\* \ldots \*m_n$
$\color{brown}{但是题目并未说m_1,m_2,\ldots,m_n之间两两互质,需要重新推导}$

推导(按题目的来)

$$\begin{cases} x \equiv m_1(mod \quad a_1) \color{red}{①}\\\\ x \equiv m_2(mod \quad a_2) \color{red}{②}\\\\ \ldots\ldots\\\\ x \equiv m_n(mod \quad a_n)\\\\ \end{cases}$$

先计算两个线性同余方程组的解,之后依此类推
$\color{brown}{①}$ 可以写成 $x=k_1 \ast a_1 + m_1 \color{red}{③}$
$\color{brown}{②}$ 可以写成 $x=k_2 \ast a_2 + m_2 \color{red}{④}$
③=④ $\longrightarrow k_1 \ast a_1 + m_1=k_2 \ast a_2 + m_2 \longrightarrow k_1 \ast a_1 - k_2 \ast a_2=m_2 - m_1 \color{red}{⑤}$
根据裴蜀定理,当$m_2 - m_1 为 gcd(a_1,-a_2) 的倍数时,方程\color{brwon}{⑤}有无穷组整数解$
而$k_1 \ast a_1 - k_2 \ast a_2 =gcd(a_1,-a_2)=d$可以用拓展欧几里得算法来解,即$exgcd(a_1,-a_2,k_1,k_2)$
$\color{blue}{如何求解k_1 \ast a_1 - k_2 \ast a_2 =gcd(a_1,-a_2)=d \quad 中的 k_1 和 k_2?}$
$\color{black}{先引入结论k_1,k_2的通解,非齐次=齐次通解+非齐次特解}$
$$ k_1 = k_1 + k \ast \frac{a_2}{d} \\\\ k_2 = k_2 + k \ast \frac{a_1}{d} $$
证明:
$k_1的通解为s_1,k_2的通解为s_2,k_1的特解为k_1,k_2的特解为k_2$
∴有$$\begin{cases} a_1 \ast s_1 - a_2 \ast s_2=d\\\\ a_1 \ast k_1 -a_2 \ast k_2=d\\\\ \end{cases}$$
$$\downarrow{\color{BlueViolet}{方程组同时除d}}$$
$$\begin{cases} \frac{a_1}{d} \ast s_1 -\frac{a_2}{d} \ast s_2=1 \color{red}{⑥}\\\\ \frac{a_1}{d} \ast k_1 - \frac{a_2}{d} \ast k_2=1\\\\ \end{cases}$$
$$\downarrow{\color{BlueViolet}{相减下}}$$
$$\frac{a_1}{d} \ast (s_1-k_1) - \frac{a_2}{d} \ast (s_2-k_2)=0$$
$$其中\frac{a_1}{d}与\frac{a_2}{d}互质 \quad -> s_1 - k_1 必然是 \frac{a_2}{d}的倍数\\\\ ∴s_1-k_1=k \ast \frac{a_2}{d} \quad -> k_1=k_1+k \ast \frac{a_2}{d} \\\\ 同理可得k_2=k_2 + k \ast \frac{a_1}{d}\\\\ 又有疑问了? \quad \color{red}{\frac{a_1}{d}与\frac{a_2}{d}为什么互质?}\\\\ 在方程组\color{brown}{⑥}中根据裴蜀定理的推论(a,b互质的充要条件是存在整数x,y使ax+by=1)\\\\ 从而得出它两互质. \\\\到此证明完毕 $$

$$回归正题,求解本题\\\\ 将k_1通解代入③\quad 得\quad\\\\ x=\underbrace{k_1 \ast a_1+m_1}_{更新后的m_1} +\overbrace{\frac{a_2}{d} \ast a_1}^{更新后的a_1}*k \\\\依此迭代,\\\\经过n-1次后可以将n个线性同余方程合并为一个方程,求最小解,只需 $$

代码 $\quad O(log(a_1 + a_2))$

#include<iostream>
using namespace std; 
long long exgcd(long a,long b,long long & x,long long & y)
{
    int d;
    if(!b)
    {
        x=1,y=0;
        return a;
    }
    d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
int main()
{
    int n;
    cin>>n;
    long long a1,m1;
    bool ias;
    cin>>a1>>m1;
    n-=1;
    while(n--)
    {
        long long a2,m2;
        long long k1,k2;
        ias=true;
        cin>>a2>>m2;
        long long  d=exgcd(a1,-a2,k1,k2);
        if((m2-m1)%d)
        {
            ias=false;
            break;
        }
        k1*=(m2-m1)/d;
        long long t=a2/d;
        k1=(k1%t+t)%t;
        m1=a1*k1+m1;
        a1=abs(a1/d*a2);
    }
    cout<<(ias==false?-1:(m1%a1+a1)%a1)<<endl;
    return 0;
}

$\color{brown}{喜欢题解的话,欢迎点赞、收藏、关注(三连)喔,如有什么疑问,欢迎评论下方指出}$