题目描述

有N块木板从左到右排成一行，有M个工匠对这些木板进行粉刷，每块木板至多被粉刷一次。

第 i 个木匠要么不粉刷，要么粉刷包含木板 $S_i$ 的，长度不超过 $L_i$ 的连续的一段木板，每粉刷一块可以得到 $P_i$ 的报酬。

不同工匠的$S_i$不同。

请问如何安排能使工匠们获得的总报酬最多。

输入格式

第一行包含两个整数N和M。

接下来M行，每行包含三个整数$L_i,P_i,S_i$。

输出格式

输出一个整数，表示结果。

数据范围

$1 \le N \le 16000$,
$1 \le M \le 100$,
$1 \le P_i \le 10000$

输入样例：

8 4
3 2 2
3 2 3
3 3 5
1 1 7 

输出样例：

17

解题报告

题意理解

一个区间的木块要粉刷,每一个木块最多只能粉刷一次,可以不粉刷,对于一个粉刷匠$i$而言,他必须粉刷第$S_i$木板,而且只能粉刷一段连续的木块,并且要求粉刷长度不超过$L_i$,而且每刷一个木板,就可以得到$P_i$的报酬,现在要求报酬最大化,

解题思路

①首先将所有粉刷匠,按照必须刷的小木块$S_i$从小到大排序.

上面这个操作为了保证我们可以顺序处理.

②我们可以设$f[i][j]$表示为,前$i$个粉刷匠,刷了前$i$个木块.可以有些木块选择不刷

状态确定好了后,我们分两种情况讨论.

1. 第$i$个粉刷匠不工作,那么
   $$f[i][j]=f[i-1][j]$$

2. 第$j$个木板不刷,那么
   $$f[i][j]=f[i][j-1]$$
   .

结合上面的讨论,我们不难发现,
$$f[i][j]=max(f[i-1][j],f[i][j-1])$$

接下来的问题就是,如果说粉刷匠工作,而且也还刷第$j$个木块,那么我们不得不仔细思考.

对于一个粉刷匠而言,如果说聘请他工作,那么显然我们有几个条件.

1. 他粉刷的区间长度,至少为$1$,最多为$L_i$.
2. 他粉刷的区间内必须包括$S_i$这个小木块.
3. 粉刷区间左端点,必须小于等于$S_i$

综上所述我们不妨设置一个粉刷匠粉刷的区域为$[k+1,j]$

那么根据上面所说的条件,我们将它转换为数学计算机语言,如下面这个式子所示.
$$k+1 \le s_i \le j \\ 1 \le j-(k+1) \le L_i \\ K \le S_i-1$$

综上所述,我们可以将状态转移方程一步步出来.

$$f[i][j]=\max{f[i-1][j],f[i][j-1],f[i][j]} \\ f[i][j]=\max_{j-L_i \le k \le S_i-1} (f[i][j],f[i-1][k]+P_i*(j-(k+1)+1)) \\ $$

得出了一个朴素的状态转移方程,我们不得不进行转换一下.

$$f[i][j]=\max_{j-L_i \le k \le S_i-1} (f[i][j],f[i-1][k]+P_i*(j-(k+1)+1)) \\ $$

我们不妨去掉一个括号.

$$f[i][j]=\max_{j-L_i \le k \le S_i-1} (f[i][j],f[i-1][k]+P_i*(j-k)) \\ $$

上面的一次次变换,让我们发现了,如果说我们要求的$f[i][j]$要选取到最大值,那么我们核心目标点就是让Max函数内部的

$$f[i-1][k]-P_i*k$$

尽量地大.

尽然如此的话,我们发现K的取值是一个范围,但是我们并不关心这个范围内所有的数值,我们唯一的关心点就是这个范围的最大值.也就是最大的$f[i-1][k]$

一个区间,最大值,这些关键字眼,不得不让我们思考一下单调队列这种优秀的数据结构.因此我们把中心放到单调队列上面.

单调队列的核心要点,就是生存能力的判断.

我们逐步入手,下面给出几个判断依据.

我们设当前有两个点,一个是$k_1$,另外一个是$k_2$.

我们发现当前点,如果说$k_1<k_2$,也就是$k_2$后出现.

我们将$k_1$,$k_2$代入到我们的状态转移方程中的决定部分.

那么将$k_1$代入

$f[i-1][k_1]-P_i * k_1$

再将$k_2$代入其中

$f[i-1][k_2]-P_i * k_2$

我们发现如果说我们再满足下面这个条件的话,那么$k_2$一定优于$k_1$

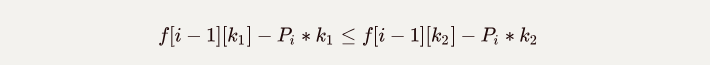
就好比如说,一个人比你小,还比你强,那么你就真的比不过他了.

代码分析

#include <bits/stdc++.h>
using namespace std;
const int M=16000+100;
const int N=110;
int n,m,i,j,k,f[N][M];
struct node
{
    int p,l,s;//单价;最高长度;必备点
} a[M];
deque<int> q;
int cmp(node a,node b)//排序
{
    return a.s<b.s;
}
void init()
{
    ios::sync_with_stdio(false);
    cin>>m>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i].l>>a[i].p>>a[i].s;
    sort(a+1,a+1+n,cmp);
}
int date(int i,int k)
{
    return f[i-1][k]-a[i].p*k;
}
void work()
{
    for(int i=1;i<=n;i++)//粉刷匠
    {
        for(int k=max(0,a[i].s-a[i].l);k<a[i].s;k++)
        {
            while (q.size() && date(i,q.back())<=date(i,k))//不是最优值
                q.pop_back();
            q.push_back(k);
        }
        for(int j=1;j<=m;j++)//粉刷墙
        {
            f[i][j]=max(f[i-1][j],f[i][j-1]);//第一步取最大值
            if (j>=a[i].s)
            {
                while(q.size() && q.front()<j-a[i].l)//不在候选范围内了.
                    q.pop_front();
                if (q.size())
                    f[i][j]=max(f[i][j],a[i].p*j+date(i,q.front()));//计算
            }
        }
    }
    cout<<f[n][m];
}
int main()
{
    init();
    work();
    return 0;
}