思路

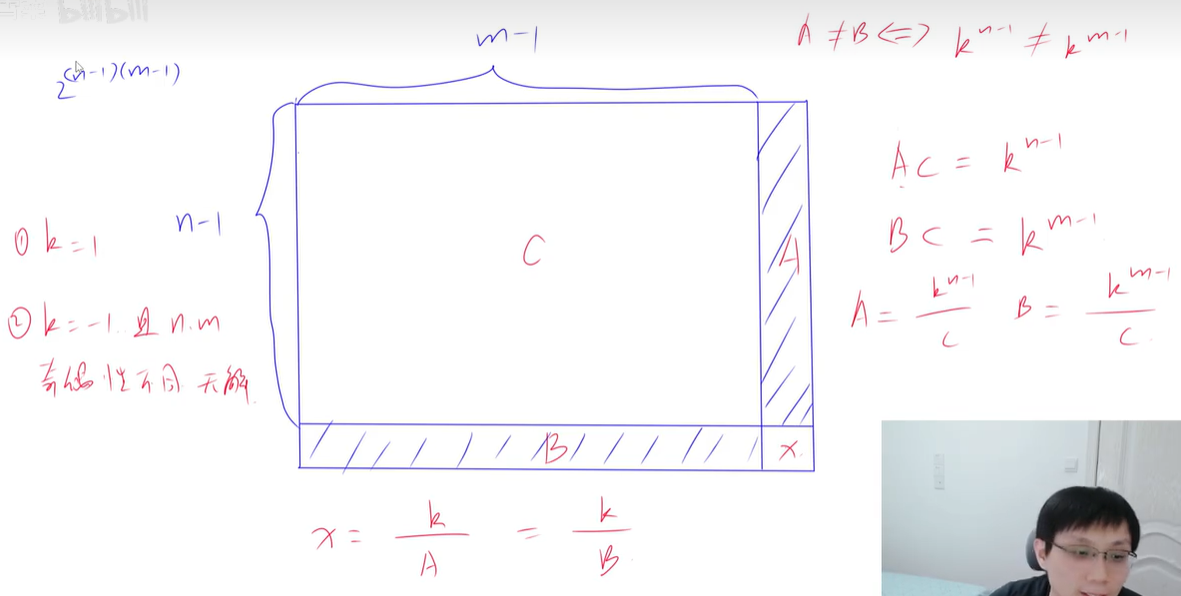
任填前 $n - 1$ 行，$m - 1$ 列，每个方格有两种选择，共 $2^{(n - 1)(m - 1)} = {(2^{n - 1})}^{m - 1}$ 种。由于每行每列乘积为 $k$，下图中区域 $A, B$ 的填法固定，进而，右下角 $x = \frac{k}{A} = \frac{k}{B}$。

若 $A = B$ 则有解，否则无解。设前 $n - 1$ 行，$m - 1$ 列的乘积为 $C$，则

$$ AC = k^{n - 1} $$

$$ BC = k^{m - 1} $$

$C \ne 0$，则 $A = B$ 等价于 $k^{n - 1} = k^{m - 1}$。当 $k = 1$ 时，等式恒成立。当 $k = -1$ 时，仅当 $n,m$ 奇偶性相同时成立。

#include <iostream>

using namespace std;

typedef long long LL;

const int MOD = 1e9 + 7;

LL n, m;
int k;

int qmi(int a, LL b) {
  int r = 1 % MOD;
  while (b) {
    if (b & 1) r = (LL)r * a % MOD;
    a = (LL)a * a % MOD;
    b >>= 1;
  }
  return r;
}

int main() {
  cin >> n >> m >> k;

  if (n + m & 1 && k == -1) cout << 0 << endl;
  else cout << qmi(qmi(2, n - 1), m - 1) << endl;

  return 0;
}