$$\color{Red}{将有序链表转换为二叉搜索树【leetcode109 平衡二叉树】}$$

我的网站=> 分享了我关于前后端的各种知识和生活美食~

我于Acwing平台分享的零散刷的各种各样的题

给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

示例 1:

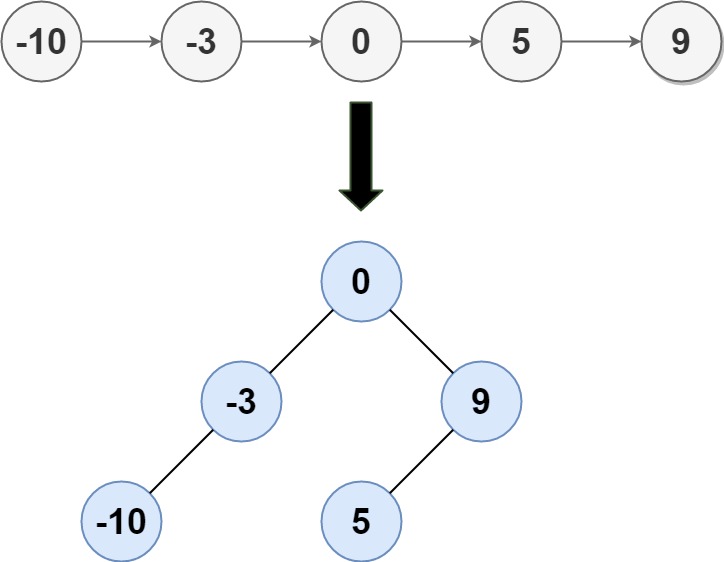
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。

示例 2:

输入: head = []
输出: []

提示:

• head 中的节点数在[0, 2 * 10^4] 范围内
• -10^5 <= Node.val <= 10^5

解析

这道题当然可以直接复制一个数组，然后通过数组能直接 O(1) 获取元素，然后变成上一道题，但是会开额外的 O(N) 空间，如果不开，就只能使用原地算法。

那么就只能通过遍历获取元素个数，然后递归的计算左右子树。

同时递归的过程中，为了能终结遍历，即锁定子树的长度，且操作前后子树，需要获取的指针指向 中间节点的前一个节点，同时需要先递归获取右子树，易忘操作左子树会让左子树的终点变成 null，如果不额外每个递归的过程中，不断开新变量提前存储右子树起点的节点，就会出现空指针。

所以先递归获取右子树，因为右子树只决定于起点的节点位置，不会改变原链表的结构。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        if (head == null) return null;
        int n = 0;
        for (ListNode p = head; p != null; p = p.next) n ++;
        if (n == 1) return new TreeNode(head.val);
        ListNode cur = head;
        for (int i = 0; i < n / 2 - 1; i ++) cur = cur.next;
        TreeNode root = new TreeNode(cur.next.val);
        root.right = sortedListToBST(cur.next.next);
        cur.next = null;
        root.left = sortedListToBST(head);
        return root;
    }
}