题目描述

给定一个非负整数 $k,(k \le 33)$，返回帕斯卡三角形的第 $k$ 行。

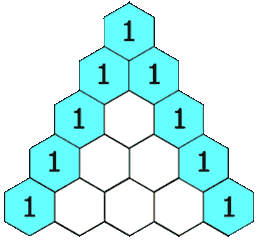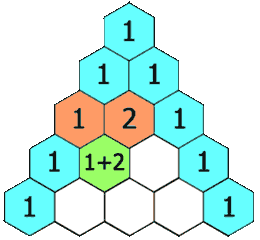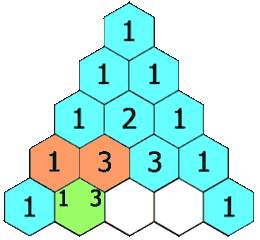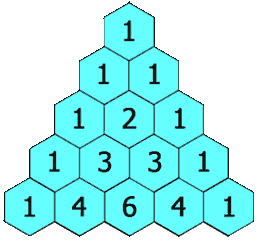
在帕斯卡三角形中，每个数是上方两个数的和。

进一步要求：能否只用 $O(k)$ 的空间？

样例

输入：3
输出：[1,3,3,1]

算法

(递推，滚动数组) $O(n^2)$

一行一行计算，由于每行的值仅与上一行的值有关，所以可以用滚动数组优化。
计算每一行的值时，先将1放在首位两个位置，然后计算中间的数：f[i][j]=f[i-1][j-1]+f[i-1][j]；

时间复杂度分析：假设行数是 $n$，则总共有 $n*(n+1)/2$ 个状态，计算每个状态的时间复杂度是 $O(1)$，所以总时间复杂度是 $O(n^2)$。

C++ 代码

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> last(rowIndex + 1), now(rowIndex + 1);
        last[0] = 1;
        for (int i = 0; i < rowIndex; i ++ )
        {
            now[0] = last[0];
            for (int j = 0; j + 1 <= i; j ++ )
                now[j + 1] = last[j] + last[j + 1];
            now[i + 1] = last[i];
            last = now;
        }
        return last;
    }
};