Codeforces Round 903 (Div. 3)[A-G]

Codeforces Round 903 (Div. 3)

A. Don’t Try to Count[暴力,模拟]

给定长度为$n$的字符串$x$和长度为$m$的字符串$s$（$n \cdot m \le 25$），由小写拉丁字母组成，您可以对字符串$x$应用任意数量的运算。在一个操作中，您将$x$的当前值附加到字符串$x$的末尾。请注意，$x$的值将在此之后更改。

例如，如果$x =$“ABA”，则在应用操作后，$x$将发生如下变化：“ABA”$\rightarrow$“ABAABA”$\rightarrow$“ABAABAABABA”。

在什么最小数量的操作之后，$s$将作为子字符串出现在$x$中？

字符串的子串被定义为它的连续段。

A题由于$25<2^6$ 所以暴力模拟五次 然后判断输出，不会$TLE$

code

#include <bits/stdc++.h>
#define int long long
int n, m;
void solve() {
  std::cin >> n >> m;
  std::string a, b;
  std::cin >> a >> b;
  int cnt = 0;
  while (cnt < 6) {
    if (a.find(b) != std::string::npos) {
      break;
    } else
      a += a;
    cnt++;
  }
  std::cout << (cnt == 6 ? -1 : cnt) << "\n";
}

signed main() {
  int __;
  std::cin >> __;
  while (__--) solve();
  return 0;
}

B. Three Threadlets[小模拟]

很久以前，酒保Decim发现了三根线和一把剪刀。在一次操作中，DECIM选择任何线程并将其切割成两个线程，

它们的长度是正整数，并且它们的和等于被切割的细线的长度。例如，他可以将长度为$5$的线程切割成长度为$2$和$3$的线程，

但是他不能把它切成长度为$2.5$和$2.5$，或者长度为$0$和$5$，或者长度为$3$和$4$的线团。DECIM可以执行最多三次操作。他被允许切割从先前的切割中获得的丝线。

他能把所有的线都做得一样长吗？

B题是个 大模拟，模拟一下 A切几刀 B切几刀 C切几刀 ，一共就一二十种情况

虽然码量很多但是复制粘贴就行

code

#include <bits/stdc++.h>
#define int long long


int n, m;
void solve() {
  int a, b, c;
  std::cin >> a >> b >> c;
  bool falg = false;
  for (int i = 0; i <= 3; i++) {
    if (i == 0) {
      if (a == b and b == c) {
        std::cout << "YES\n";
        falg = true;
        break;
      }
    } else if (i == 1) {
      int avg = (a + b + c) / 4;
      if (avg * 4 == a + b + c) {
        if (a == avg * 2 and b == c) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (b == avg * 2 and a == c) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (c == avg * 2 and b == a) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
      }
    } else if (i == 2) {
      int avg = (a + b + c) / 5;
      if (avg * 5 == a + b + c) {
        if (a == avg * 3 and b == c) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (b == avg * 3 and a == c) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (c == avg * 3 and b == a) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 2 and a == b) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 2 and a == c) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (b == avg * 2 and c == b) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
      }
    } else if (i == 3) {
      int avg = (a + b + c) / 6;
      if (avg * 6 == a + b + c) {
        if (a == avg * 4 and b == c) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (b == avg * 4 and a == c) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (c == avg * 4 and b == a) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 3 and b == avg * 2 and c == avg * 1) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 3 and b == avg * 1 and c == avg * 2) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 2 and b == avg * 1 and c == avg * 3) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 2 and b == avg * 2 and c == avg * 2) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 2 and b == avg * 3 and c == avg * 1) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 1 and b == avg * 2 and c == avg * 3) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
        if (a == avg * 1 and b == avg * 3 and c == avg * 2) {
          std::cout << "YES\n";
          falg = true;
          break;
        }
      }
    }
  }
  if (!falg) {
    std::cout << "NO\n";
  }
}

signed main() {
  int __;
  std::cin >> __;
  while (__--) solve();
  return 0;
}

C. Perfect Square[模拟]

Kristina有一个大小为$n$乘以$n$的矩阵，其中填充了小写的拉丁字母。$n$的值是偶数。她想改变一些字符，使她的矩阵成为一个完美的正方形。

如果一个矩阵在顺时针旋转$90^\circ$一次时保持不变，则称该矩阵为完全正方形。

下面是将矩阵旋转$90^\circ$的示例：

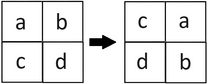
在一个操作中，Kristina可以选择任何单元格，并用字母表中的下一个字符替换其值。

如果字符等于“Z”，则其值不变。找出使矩阵成为完全正方形所需的最小运算次数。

例如，如果$4$乘$4$矩阵如下所示：

$$ \matrix{ a & b & b & a \cr b & c & \textbf{b} & b \cr b & c & c & b\cr a & b & b & a \cr } $$

然后，将$1$操作应用于字母B（以粗体突出显示）即可。

C题有一个坑点，就是每次只能将字母变大，而且只能变大1，也就是变成后面一个字母

题目中的性质是矩阵旋转九十度后不变

那么我们推广一下，也就是90度再90度也不变

90度再90度再90度也不变，90度再90度再90度再90度也不变

于是一个位置一共有三个对应的位置，我们找出这四个字母

又因为字母只能变大一

所以我们就让三个字母变成最大的一个

然后将最大值-当前字母存储到答案中

遍历一遍即可

如果是1~n * 1~n 这样枚举的话

那么 对应的四个位置的贡献会计算四次

所以要在答案上除以4输出

然后就可以解决掉C

code

#include <bits/stdc++.h>
#define int long long
int n, m;

void rotatePoint(int n, int x, int y, int &rotatedX, int &rotatedY) {
  rotatedX = y;
  rotatedY = n - 1 - x;
}
void solve() {
  std::cin >> n;
  std::vector<std::vector<char>> arr(n, std::vector<char>(n));
  for (auto &i : arr) {
    for (auto &j : i) {
      std::cin >> j;
    }
  }
  int ans = 0;
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      int nx1 = i, ny1 = j;
      int nx2 = i, ny2 = j;
      rotatePoint(n, nx1, ny1, nx2, ny2);
      int nx3 = i, ny3 = j;
      rotatePoint(n, nx2, ny2, nx3, ny3);
      int nx4 = i, ny4 = j;
      rotatePoint(n, nx3, ny3, nx4, ny4);
      int bb = std::max(
          {arr[nx1][ny1], arr[nx2][ny2], arr[nx3][ny3], arr[nx4][ny4]});
      ans += abs(arr[nx1][ny1] - bb);
      ans += abs(arr[nx2][ny2] - bb);
      ans += abs(arr[nx3][ny3] - bb);
      ans += abs(arr[nx4][ny4] - bb);
    }
  }
  std::cout << ans / 4 << "\n";
}

signed main() {
  int __;
  std::cin >> __;
  while (__--) solve();
  return 0;
}

D. Divide and Equalize[分解质因子]

给定一个由$n$个正整数组成的数组$a$。您可以对其执行以下操作：

选择一对元素$a_i$和$a_j$（$1 \le i, j \le n$和$i \neq j$）

1. 选择整数$a_i$的约数之一，即整数$x$，使得$a_i \bmod x = 0$

3.将$a_i$替换为$\frac{a_i}{x}$，将$a_j$替换为$a_j \cdot x$。确定是否可以通过应用一定次数（可能为零）的操作来使数组中的所有元素相同。

例如，让我们考虑具有$5$个元素的数组$a$=[$100, 2, 50, 10, 1$]。对其执行两个操作：

1. 选择$a_3 = 50$和$a_2 = 2$，$x = 5$。

将$a_3$替换为$\frac{a_3}{x} = \frac{50}{5} = 10$，将$a_2$替换为$a_2 \cdot x = 2 \cdot 5 = 10$。结果数组为$a$=[$100, 10, 10, 10, 1$]

1. 选择$a_1 = 100$和$a_5 = 1$，$x = 10$。将$a_1$替换为$\frac{a_1}{x} = \frac{100}{10} = 10$，将$a_5$替换为$a_5 \cdot x = 1 \cdot 10 = 10$。结果数组为$a$=[$10, 10, 10, 10, 10$]。执行这些操作后，数组$a$中的所有元素都等于$10$。

D是 可以将一个数字的因子转移到另一个上，看看能不能把所有数都变成一样的

然后我们 对每个数分解质因子进行统计 因子的数量

最后 看看每个因子的数量是不是能被 n 整除

如果有一个因子 不能 整除 那就是无法均匀分配， 就输出NO

如果所有的因子都能整除 就输出YES

然后就可以解决掉D

code

#include <bits/stdc++.h>
#define int long long
int n, m;
using PII = std::pair<int, int>;
void solve() {
  std::cin >> n;
  std::vector<int> a(n);
  for (auto &i : a) {
    std::cin >> i;
  }
  std::map<int, int> mp;
  for (int t = 0; t < n; t++) {
    int &x = a[t];
    for (int i = 2; i <= x / i; i++)
      if (x % i == 0) {
        int s = 0;
        while (x % i == 0) x /= i, s++;
        mp[i] += s;
      }
    if (x > 1) mp[x]++;
  }
  for (auto [a, b] : mp) {
    if (b % n) {
      std::cout << "NO\n";
      return;
    }
  }
  std::cout << "YES\n";
}

signed main() {
  int __;
  std::cin >> __;
  while (__--) solve();
  return 0;
}

E. Block Sequence[线性DP]

给定一个长度为$n$的整数序列$a$。一个序列被称为美丽的，如果它具有一系列块的形式，每个块以其长度开始，即

首先是块的长度，然后是它的元素。例如，序列[$\color{red}{3},\ \color{red}{3},\ \color{red}{4},\ \color{red}{5},\ \color{green}{2},\ \color{green}{6},\ \color{green}{1}$]和[$\color{red}{1},\ \color{red}{8},\ \color{green}{4},\ \color{green}{5},\ \color{green}{2},\ \color{green}{6},\ \color{green}{1}$]是漂亮的（不同的块具有不同的颜色），而[$1$]、[ $1,\ 4,\ 3$}]、[$3,\ 2,\ 1$]则不是。在一个操作中，您可以从序列中删除任何元素。

要使给定的序列美观，最少需要多少次操作？

E 题是个 线性DP

通过观察我们可以发现 它的最优子结构和无后效性

对于一个位置删不删除，删除的话就是 前一位的答案 加上 一

不删除的话 就将前一位的答案 转移到 下标加当前值的地方

最后看看 n+1 的地方能不能被转移到

输出dp[n+1]的值即可

code

#include <bits/stdc++.h>
#define int long long
int n, m;
void solve() {
  std::cin >> n;
  std::vector<int> a(n + 1);
  std::vector<int> dp(n + 10, INT_MAX);
  dp[1] = 0;
  for (int i = 1; i <= n; i++) {
    std::cin >> a[i];
  }
  for (int i = 1; i <= n; i++) {
    dp[i] = std::min({dp[i], dp[i - 1] + 1});
    if (i + a[i] + 1 <= n + 1)
      dp[i + a[i] + 1] = std::min(dp[i], dp[i + a[i] + 1]);
  }
  dp[n + 1] = std::min(dp[n + 1], dp[n] + 1);
  std::cout << dp[n + 1] << "\n";
}

signed main() {
  int __;
  std::cin >> __;
  while (__--) solve();
  return 0;
}

F. Minimum Maximum Distance[树的直径]

您有一棵具有 $n$ 个顶点的树，其中一些顶点已标记。树是没有圈的连通无向图。令 $f_i$ 表示从顶点 $i$ 到任何标记顶点的最大距离。

你的任务是在所有顶点中找出 $f_i$ 的最小值。

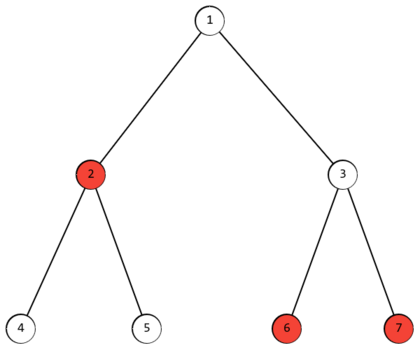
例如，在示例中显示的树中，标记了顶点 $2$ 、 $6$ 和 $7$ 。然后是数组 $f(i) = [2, 3, 2, 4, 4, 3, 3]$ 。

最小值 $f_i$ 用于顶点 $1$ 和 $3$ 。

确定树的直径可以用两次bfs处理

一次从根开始找最远点

一次从最远点找最远点的最远点

code

#include <bits/stdc++.h>
#define int long long
int n, m;
void solve() {
  std::cin >> n >> m;
  std::vector<int> col(n);
  std::vector<int> tt(m);
  std::vector<std::vector<int>> G;
  G.resize(n);
  for (auto &i : tt) {
    std::cin >> i;
    i--;
    col[i]++;
  }
  for (int i = 1; i < n; i++) {
    int x, y;
    std::cin >> x >> y;
    x--, y--;
    G[x].emplace_back(y);
    G[y].emplace_back(x);
  }
  std::vector<int> dist(n, -1);
  auto bfs = [&](int u) -> int {
    dist = std::vector<int>(n, -1);
    std::queue<int> q;
    q.push(u);
    dist[u] = 0;
    while (!q.empty()) {
      auto t = q.front();
      q.pop();
      for (auto it : G[t]) {
        if (!~dist[it]) {
          dist[it] = dist[t] + 1;
          q.push(it);
        }
      }
    }
    int t = -1;
    for (int i = 0; i < n; i++) {
      if (col[i] and (!~t or dist[i] > dist[t])) {
        t = i;
      }
    }
    return t;
  };
  int b = bfs(0);
  int a = bfs(b);
  auto t = dist;
  bfs(a);
  for (int i = 0; i < n; i++) {
    t[i] = std::max(t[i], dist[i]);
  }
  std::cout << *min_element(begin(t), end(t)) << "\n";
}

signed main() {
  int __;
  std::cin >> __;
  while (__--) solve();
  return 0;
}

G. Anya and the Mysterious String[线段树]

安雅收到了从罗马带来的长度为 $n$ 的字符串 $s$ 。字符串 $s$ 由小写的拉丁字母组成，乍一看不会引起任何怀疑。一条指令被附加到字符串上。指令的开始。

回文是从左到右和从右到左读起来都相同的字符串。

例如，字符串“Anna”、“Aboba”、“Level”是回文，而字符串“Gorilla”、“Banan”和“Off”则不是回文。字符串 $s$ 的子字符串 $[l \ldots r]$ 是字符串 $s_l s_{l+1} \ldots s_{r-1} s_r$ 。例如，字符串“generation”的子字符串 $[4 \ldots 6]$ 是字符串“era”。

如果一个字符串不包含长度至少为**2的回文子串，则称该字符串为Beautiful。

例如，字符串“FOX”、“ABCDEF”和“YIOY”很漂亮，而字符串“XYXX”、“YIKJKITRB”则不漂亮。当整数 $x$ 添加到字符 $s_i$ 时，它将被字母表中的下一个字符替换 $x$ 次。

其中“Z”被“A”代替。将整数 $x$ 添加到字符串 $s$ 的子字符串 $[l, r]$ 时，它将变为字符串 $s_1 s_2 \ldots s_{l-1} (s_l + x) (s_{l+1} + x) \ldots (s_{r-1} + x) (s_r + x) s_{r+1} \ldots s_n$ 。

例如，当字符串“abazaba”的子字符串 $[2, 4]$ 加上数字 $6$ 时，得到的字符串是“ahgfaba”。指令结束。

读完说明后，安雅接受了她必须回答 $m$ 个问题的事实。

查询可以是两种类型：

1. 将数字 $x$ 添加到字符串 $s$ 的子字符串 $[l \ldots r]$ 。

判断字符串 $s$ 的子字符串 $[l \ldots r]$ 是否美观。

只跟踪长度为 $2$ 和$ 3$ 的回文

线段树维护区间加 区间合法性查询

code

#include <bits/stdc++.h>
#define int long long
int n, m;
template <class Info, class Tag>
struct LazySegmentTree {
  int n;
  std::vector<Info> info;
  std::vector<Tag> tag;
  LazySegmentTree() : n(0) {}
  LazySegmentTree(int n_, Info v_ = Info()) { init(n_, v_); }
  template <class T>
  LazySegmentTree(std::vector<T> init_) {
    init(init_);
  }
  void init(int n_, Info v_ = Info()) { init(std::vector<Info>(n_, v_)); }
  template <class T>
  void init(std::vector<T> init_) {
    n = init_.size();
    info.assign(4 << std::__lg(n), Info());
    tag.assign(4 << std::__lg(n), Tag());
    std::function<void(int, int, int)> build = [&](int p, int l, int r) {
      if (r - l == 1) {
        info[p] = init_[l];
        return;
      }
      int m = (l + r) / 2;
      build(2 * p, l, m);
      build(2 * p + 1, m, r);
      pull(p);
    };
    build(1, 0, n);
  }
  void pull(int p) { info[p] = info[2 * p] + info[2 * p + 1]; }
  void apply(int p, const Tag &v) {
    info[p].apply(v);
    tag[p].apply(v);
  }
  void push(int p) {
    apply(2 * p, tag[p]);
    apply(2 * p + 1, tag[p]);
    tag[p] = Tag();
  }
  void modify(int p, int l, int r, int x, const Info &v) {
    if (r - l == 1) {
      info[p] = v;
      return;
    }
    int m = (l + r) / 2;
    push(p);
    if (x < m) {
      modify(2 * p, l, m, x, v);
    } else {
      modify(2 * p + 1, m, r, x, v);
    }
    pull(p);
  }
  void modify(int p, const Info &v) { modify(1, 0, n, p, v); }
  Info rangeQuery(int p, int l, int r, int x, int y) {
    if (l >= y || r <= x) {
      return Info();
    }
    if (l >= x && r <= y) {
      return info[p];
    }
    int m = (l + r) / 2;
    push(p);
    return rangeQuery(2 * p, l, m, x, y) + rangeQuery(2 * p + 1, m, r, x, y);
  }
  Info rangeQuery(int l, int r) { return rangeQuery(1, 0, n, l, r); }
  void rangeApply(int p, int l, int r, int x, int y, const Tag &v) {
    if (l >= y || r <= x) {
      return;
    }
    if (l >= x && r <= y) {
      apply(p, v);
      return;
    }
    int m = (l + r) / 2;
    push(p);
    rangeApply(2 * p, l, m, x, y, v);
    rangeApply(2 * p + 1, m, r, x, y, v);
    pull(p);
  }
  void rangeApply(int l, int r, const Tag &v) {
    return rangeApply(1, 0, n, l, r, v);
  }
  template <class F>
  int findFirst(int p, int l, int r, int x, int y, F pred) {
    if (l >= y || r <= x || !pred(info[p])) {
      return -1;
    }
    if (r - l == 1) {
      return l;
    }
    int m = (l + r) / 2;
    push(p);
    int res = findFirst(2 * p, l, m, x, y, pred);
    if (res == -1) {
      res = findFirst(2 * p + 1, m, r, x, y, pred);
    }
    return res;
  }
  template <class F>
  int findFirst(int l, int r, F pred) {
    return findFirst(1, 0, n, l, r, pred);
  }
  template <class F>
  int findLast(int p, int l, int r, int x, int y, F pred) {
    if (l >= y || r <= x || !pred(info[p])) {
      return -1;
    }
    if (r - l == 1) {
      return l;
    }
    int m = (l + r) / 2;
    push(p);
    int res = findLast(2 * p + 1, m, r, x, y, pred);
    if (res == -1) {
      res = findLast(2 * p, l, m, x, y, pred);
    }
    return res;
  }
  template <class F>
  int findLast(int l, int r, F pred) {
    return findLast(1, 0, n, l, r, pred);
  }
};  // 懒标记线段树
struct Tag {
  int x = 0;  // 初始为0，表示无操作

  void apply(const Tag &t) & {
    // 将新的异或值与之前的异或值进行合并
    x += t.x;
    x %= 26;
  }
};

struct Info {
  std::array<int, 2> L = {-1, -1};
  std::array<int, 2> R = {-1, -1};
  bool ok = true;
  void apply(const Tag &t) & {
    // 对信息节点应用标记，执行异或操作
    for (auto &i : L) {
      if (i == -1) continue;
      i += t.x;
      i %= 26;
    }
    for (auto &i : R) {
      if (i == -1) continue;
      i += t.x;
      i %= 26;
    }
  }
};

Info operator+(const Info &a, const Info &b) {
  // 合并两个信息节点
  Info c;
  c.ok = a.ok and b.ok;
  if (a.R[0] == b.L[0] and a.R[0] != -1) {
    c.ok = false;
  }
  if (a.R[0] == b.L[1] and a.R[0] != -1) {
    c.ok = false;
  }
  if (a.R[1] == b.L[0] and a.R[1] != -1) {
    c.ok = false;
  }
  if (a.L[0] == -1) {
    c.L = b.L;
  } else if (a.L[1] == -1) {
    c.L[0] = a.L[0];
    c.L[1] = b.L[0];
  } else
    c.L = a.L;
  if (b.R[0] == -1) {
    c.R = a.R;
  } else if (b.R[1] == -1) {
    c.R[0] = b.R[0];
    c.R[1] = a.R[0];
  } else
    c.R = b.R;
  return c;
}
void solve() {
  std::cin >> n >> m;
  std::string s;
  std::cin >> s;
  std::vector<Info> init(n);
  for (int i = 0; i < n; i++) {
    init[i].L[0] = init[i].R[0] = s[i] - 'a';
  }
  LazySegmentTree<Info, Tag> segment(init);
  while (m--) {
    int op, l, r;
    std::cin >> op >> l >> r;
    l--;
    if (op == 1) {
      int x;
      std::cin >> x;
      segment.rangeApply(l, r, {x});
    } else {
      if (segment.rangeQuery(l, r).ok) {
        std::cout << "YES\n";
      } else {
        std::cout << "NO\n";
      }
    }
  }
}

signed main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(0), std::cout.tie(0);
  std::cout << std::fixed << std::setprecision(15);
  std::cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
  int __;
  std::cin >> __;
  while (__--) solve();
  return 0;
}