对于每种打通道路的方案，打通每条道路的先后顺序不影响结果，所以我们可以先打通深度小的结点再打通深度大的结点，这样问题就具有了动态规划的无后效性。
本题具有最优子结构性质，但是证明较繁琐，可以去看 y 总的视频，讲的非常清晰。
总之，这题可以使用动态规划来求解，根据数据范围和题目的性质可以推测需要使用状态压缩动态规划。
状态定义：$dp[i][o]$ 表示 所有选取了 $i$ 层，点的选取状态压缩为二进制数字 $o$ 的选法 构成的集合，属性为选取这些点的代价的最小值。
状态计算：前 $i$ 层的状态可以从前 $i-1$ 层转移。$dp[i][o_u]$ 可以从 $dp[i-1][o_v]$ 转移，则 $o_v$ 中所有元素在 $o_u$ 中都有，即为 ov & ou == ov。则有：
$$dp[i][ou] = \min (dp[i-1][ov] + (i-1) * cost)$$
其中 $cost$ 表示从集合 $ov$ 扩展到 $ou$ 的代价和的最小值，特别的，如果无法扩展（不满足子集条件或者无道路），则记为无穷大。考虑如何计算这个最小值：
1. 先计算每个点 $u$ 连接到集合 $o$ 的代价的最小值 $f[u][o]$，对于每个点 $O(n)$ 扫描一遍即可。
2. 对于转移方程中的 $o_u, o_v$，求出 $o_u$ 多打通的结点构成的集合 $o_r$，or = ov ^ ou，然后计算 $o_r$ 中每个元素到 $o_v$ 的最小值，求和就是整个集合连到 $o_v$ 的最小值，即为 $cost$。
初始状态是 $dp[1][2^{u-1}] = 0$，最后答案是 $\min(dp[i][2^n-1]), i \in [1,n]$。

最后补一张闫式 DP 分析法的图，方便复习：

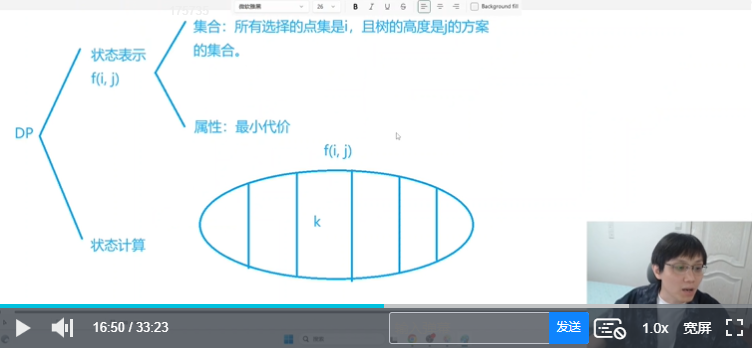
代码： 打卡记录

彩蛋：我被一个只有一个点（结点）的图卡了一个点（测试点），so，请记住：题目未明说者皆无不可能。