AcWing不会上传图片，先看这个吧

圆方树的引入

我们知道，图没有很好的性质，而树有很多性质，并且容易通过很多方式来维护树上信息，因此将图上问题转化为树上问题是我们想要解决的。圆方树就是将图转化为树的数据结构。

圆方树的分类

圆方树分为两类：狭义圆方树，广义圆方树。

狭义圆方树

狭义圆方树是可以用来将仙人掌图转化为树的一种数据结构。

广义圆方树

广义圆方树是可以用来将所有无向图转化为树的一种数据结构。

狭义圆方树

作者还没学广义圆方树，所以先来讲狭义圆方树。

仙人掌图

什么是仙人掌图？这里给出定义：

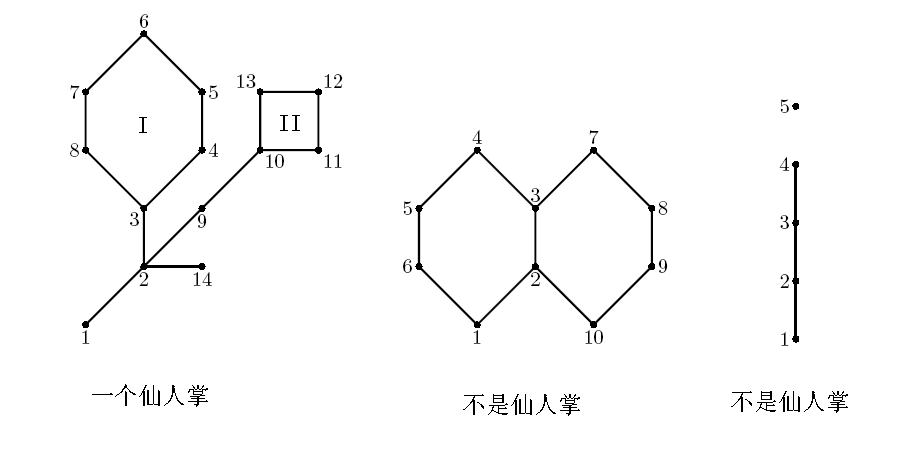
任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。

简单来说，就是图中有环并且图中任意两个环没有公共边的图。

如果你还不懂的话请看下图。

建树

我们回顾 Tarjan 算法。

在无向图中，Tarjan 算法找到图中的环，并且将环缩成一个点，这样就将原来的无向图变成了一棵树。

那这里你可能会问，那我还要圆方树干嘛，有 Tarjan 不就够了吗？还真不行，因为 Tarjan 将环都缩成一个点了，因此原来环上的很多信息你都没有办法保留了，所以在面对很多问题时就用不了了。

但是 Tarjan 算法给我们启发：可以将环看成一个整体。

于是产生了圆方树。

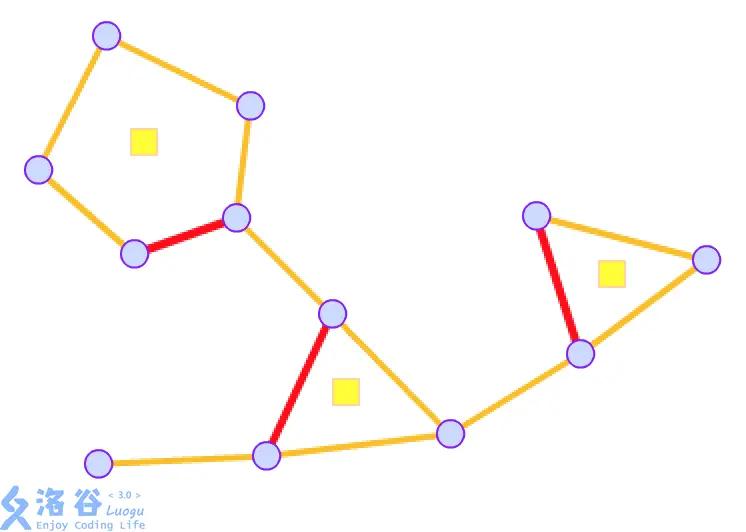
如图，原图中的每一个点看作一个圆点，而每一个环看作一个方点。

这时候我们将原来的边删去，每个圆点与它所在的环对应的方点之间连一条边，这就建好了一棵圆方树。

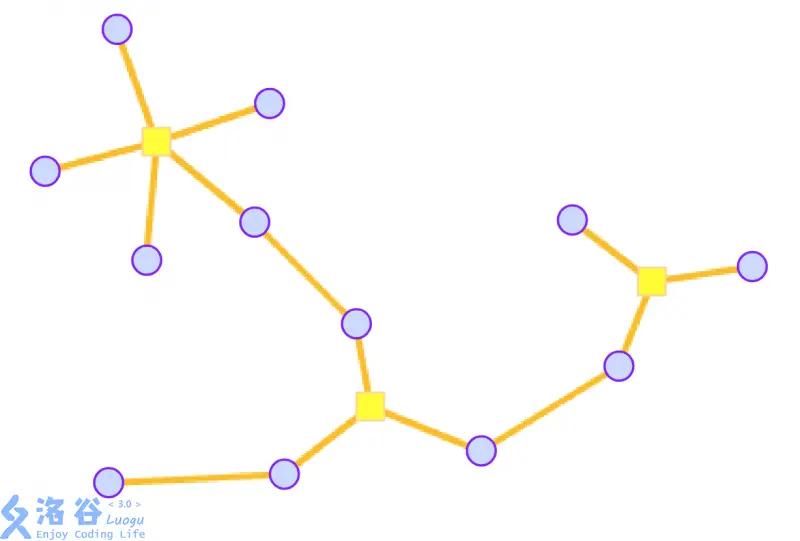
由于仙人掌图保证图中没有两个环有公共边，因此圆方树中也就不会有两个相邻的方点。

那么这个时候你可能会问，你这圆方树没有边权啊，我们这就来解决边权问题。

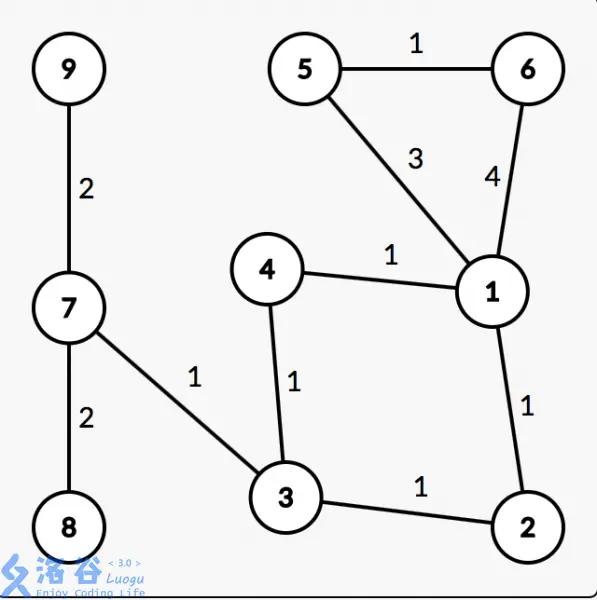
如图所示，我们设 $7$ 号节点为根节点。

图中 $3$ 号节点就是环内距离根节点最近的点。像这样距离根节点最近的点，我们令它为 $X$ 节点。

那么就有一条性质：环上各点到根节点一定经过 $X$ 节点。

环内各点到 $X$ 节点有两种方向，一种是顺时针，另一种是逆时针。而这两种方向对应的路径一定是环内各点到 $X$ 节点的最短路以及最长路。

一般来说，我们不需要维护最长路的信息，因此我们只保留最短路的信息，就像下面这棵圆方树。

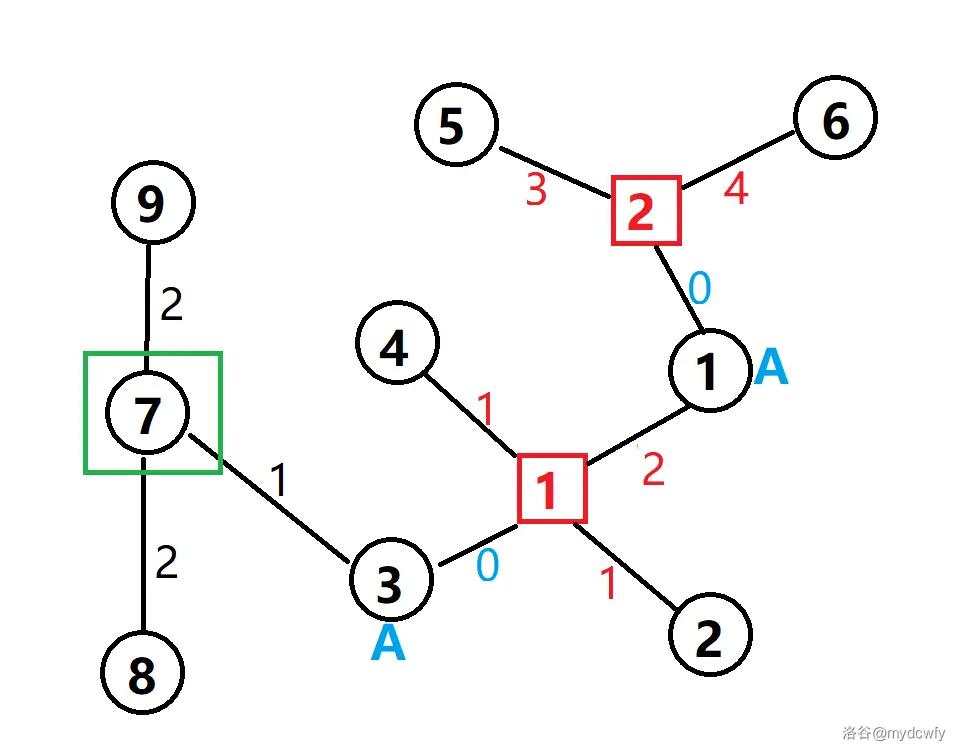
原图中 $1$ 到 $3$ 的最短路径是 $1-4-3$，长度为 $2$，圆方树上 $1$ 到 $3$ 的距离也是 $2$，就是说我们保留的信息无误。

具体实现

在 Tarjan 算法中，我们找环用的是边双连通分量，边双连通分量是指将割边删除后的连通块。

那么我们发现原图中的 $1 \sim 6$ 这 $6$ 个点都属于边双连通分量。但是它们并不属于同一个环啊，因此我们需要改进 Tarjan 算法。

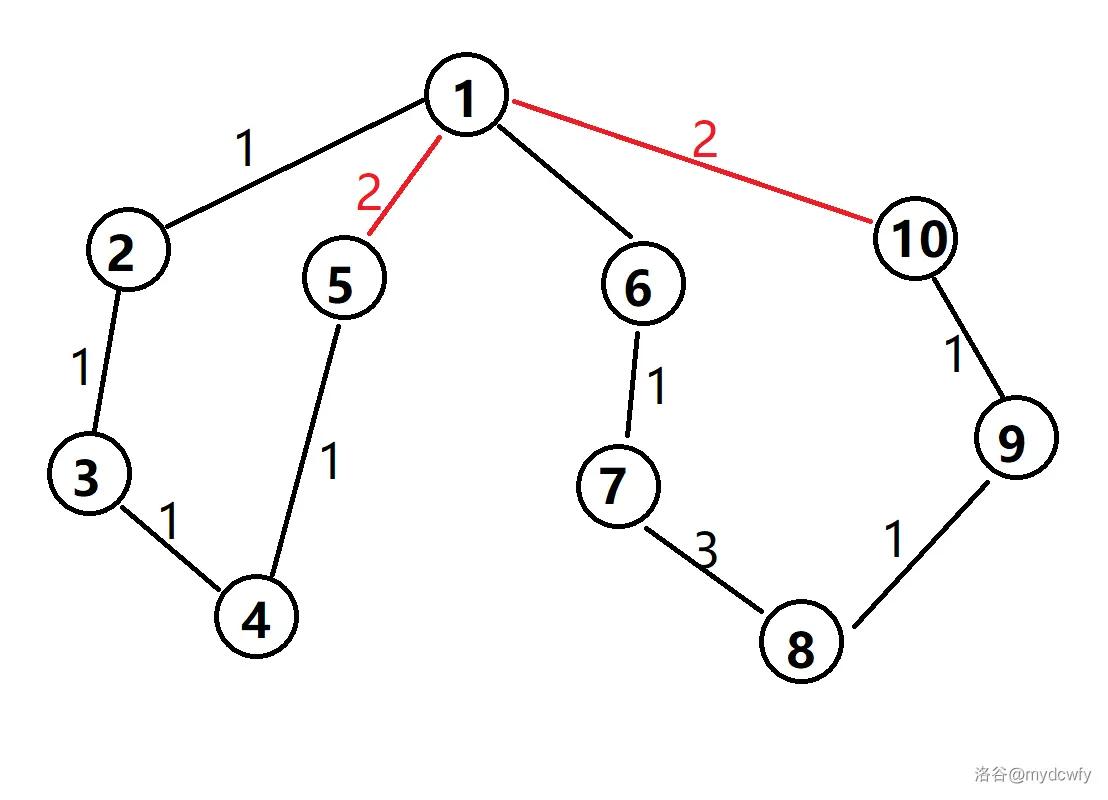
如图所示，黑色边是 Tarjan 的搜索树，红色边是非树边，即没有被遍历的边。

对于每个点，我们存储每个点的父亲，同时我们将这个点到它父亲的边的边权给这个点。

如果 $dfn_x<dfn_y$，说明 $x$ 比 $y$ 先被遍历，同时如果 $fa_y\ne x$，说明 $x$ 到 $y$ 不止一条路径，即存在环，那么我们就成功找到环了。就像上图中 $1$ 和 $5$ 之间的关系。

然后就像上面说的一样建边就好了。

接下来该处理边权问题。

由于我们找到了环，因此我们在环内绕着一个方向一直走，这样我们可以得到每个点沿着这个方向到达 $X$ 节点的距离 $dis_i$ 以及整个环的长度 $d$。

那么我们之前说了，顺时针和逆时针走对应的长度是最长路以及最短路，因此我们要保留最短路只需要比较当前节点到 $X$ 节点的距离以及用环长减去当前距离就是最短路了。

即：

$$\min(dis_i,d-dis_i)$$

然后就成功拿下圆方树了。

各种毒瘤组合

前面说了，圆方树将图上问题转化为树上问题，然后就可以套各种各样的毒瘤算法。

• 点分治

• 树上公共祖先

• 树链剖分

• 动态树

• $\ldots$

例题

P5236 【模板】静态仙人掌/AcWing 360. Freda的传呼机

题目描述

给你一个有 $n$ 个点和 $m$ 条边的仙人掌图，和 $q$ 组询问，每次询问两个点 $x,y$，求两点之间的最短路。

具体思路

首先我们先建一棵圆方树，那么问题就转化为在树上求最短路。显然 LCA 啊。

• 若 $LCA(x,y)$ 是圆点，那么这个点是原图上的点，直接就 $LCA$ 即可。

• 若 $LCA(x,y)$ 是方点，那么这个点不属于原图，我们需要将方点转化为圆点。

容易想到的是求出这个方点的两个儿子 $lc$ 和 $rc$，这个用倍增算法很容易求出。

那么问题转化为：

$$dis(x,y)=dis(x,lc)+dis(y,rc)+dis(lc,rc)$$

$dis(x,lc)$ 和 $dis(y,rc)$ 用倍增就可以解决，而 $dis(lc,rc)$ 我们在建圆方树时就已经求出了。

Code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
struct edge{int x,y,c,pre;}a[4*N];
int last[N],alen,head[N];
void ins(int x,int y,int c){
    a[++alen]=edge{x,y,c,last[x]};
    last[x]=alen;
}
void add(int x,int y,int c){
    a[++alen]=edge{x,y,c,head[x]};
    head[x]=alen;
}
int dfn[N],low[N],id;
int fa[N],w[N],cnt,s[N],len[N];
void build(int x,int y,int c){
    int d=c;//d是环上总距离 
    for(int i=y;i!=x;i=fa[i]){
        s[i]=d;//s数组是先处理所有点绕同一方向到x的距离 
        d=d+w[i];
    }
    s[x]=len[x]=d;//len数组是告诉环内每个节点，环长都是d 
    add(x,++cnt,0);
    for(int i=y;i!=x;i=fa[i]){
        len[i]=d;
        add(cnt,i,min(s[i],d-s[i]));//边权为最短路径 
    }
}
void tarjan(int x,int in_edge){
    dfn[x]=low[x]=++id;
    for(int k=last[x];k;k=a[k].pre){
        int y=a[k].y;
        if(!dfn[y]){
            fa[y]=x,w[y]=a[k].c;
            tarjan(y,k);
            low[x]=min(low[x],low[y]);
            if(dfn[x]<low[y]){
                add(x,y,a[k].c);//割边，需要连着环外的其他点 
            }
        }
        else if(k!=(in_edge^1)){
            low[x]=min(low[x],dfn[y]);
        }
    }
    for(int k=last[x];k;k=a[k].pre){
        int y=a[k].y;
        if(dfn[x]<dfn[y]&&fa[y]!=x){//找到了环 
            build(x,y,a[k].c);
        }
    }
}
struct trnode{
    int dep,dis,par[20];
    trnode(){
        dep=dis=0;
        memset(par,0,sizeof(par));
    }
}tr[N];
void dfs(int x,int fa,int c){
    tr[x].dep=tr[fa].dep+1;
    tr[x].dis=tr[fa].dis+c;
    tr[x].par[0]=fa;
    for(int i=1;i<=19;i++){
        tr[x].par[i]=tr[tr[x].par[i-1]].par[i-1];
    }
    for(int k=head[x];k;k=a[k].pre){
        int y=a[k].y;
        if(y!=fa){
            dfs(y,x,a[k].c);
        }
    }
}
int lc,rc;
int LCA(int x,int y){
    if(tr[x].dep<tr[y].dep)swap(x,y);
    for(int i=19;i>=0;i--){
        if(tr[x].dep-(1<<i)>=tr[y].dep){
            x=tr[x].par[i];
        }
    }
    if(x==y)return y;
    for(int i=19;i>=0;i--){
        if(tr[x].par[i]!=tr[y].par[i]){
            x=tr[x].par[i];
            y=tr[y].par[i];
        }
    }
    lc=x,rc=y;//lc和rc是x,y在环上祖先 
    return tr[x].par[0];
}
int main(){
    int n,m,q;scanf("%d%d%d",&n,&m,&q);
    cnt=n;//方点的编号从n+1开始 
    alen=1;memset(last,0,sizeof(last));
    memset(head,0,sizeof(head));
    for(int i=1;i<=m;i++){
        int x,y,c;scanf("%d%d%d",&x,&y,&c);
        ins(x,y,c),ins(y,x,c);
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i])tarjan(i,0);
    }
    dfs(1,0,0);
    for(int i=1;i<=q;i++){
        int x,y;scanf("%d%d",&x,&y);
        int lca=LCA(x,y);
        if(lca<=n){
            //说明x,y祖先时是圆点 
            printf("%d\n",tr[x].dis+tr[y].dis-2*tr[lca].dis);
        }
        else{
            //说明x,y祖先是方点，要转化为圆点之间的问题
            //dis(x,y)=dis(x,lc)+dis(y,rc)+dis(lc,rc) 
            int dis1=tr[x].dis-tr[lc].dis,dis2=tr[y].dis-tr[rc].dis;
            int dis3=min(abs(s[lc]-s[rc]),len[lc]-abs(s[lc]-s[rc]));
            printf("%d\n",dis1+dis2+dis3);
        }
    }
    return 0;
}