判断边是否应该加入到集合中
这是当前的全部集合,此时总集合边的数量为4
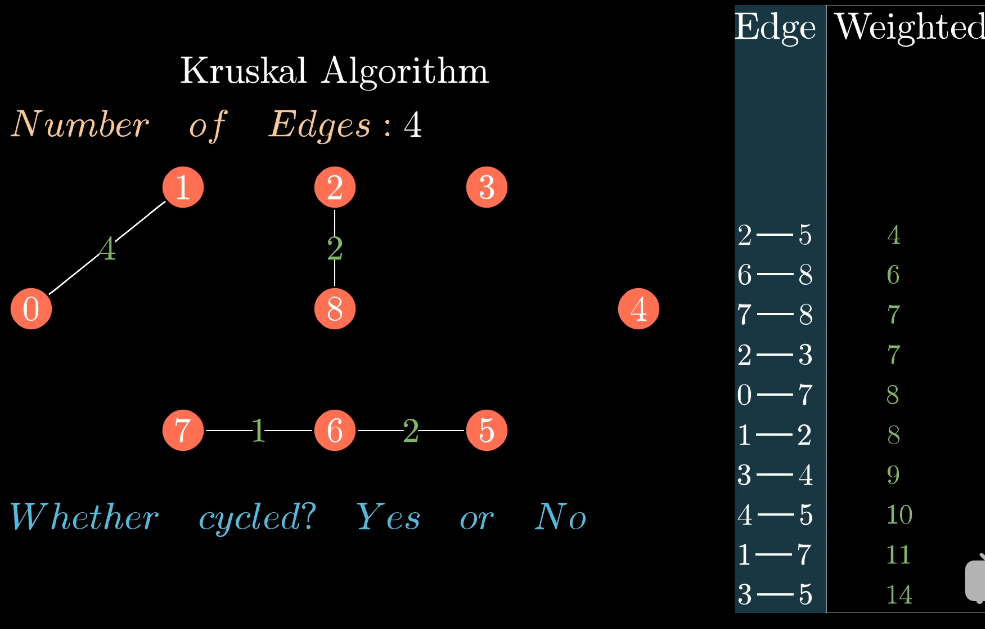
此时我们可以看到2-5这条边的值最小,因为2所在的集合与5所在的集合不同,所以可以连接,边数加1
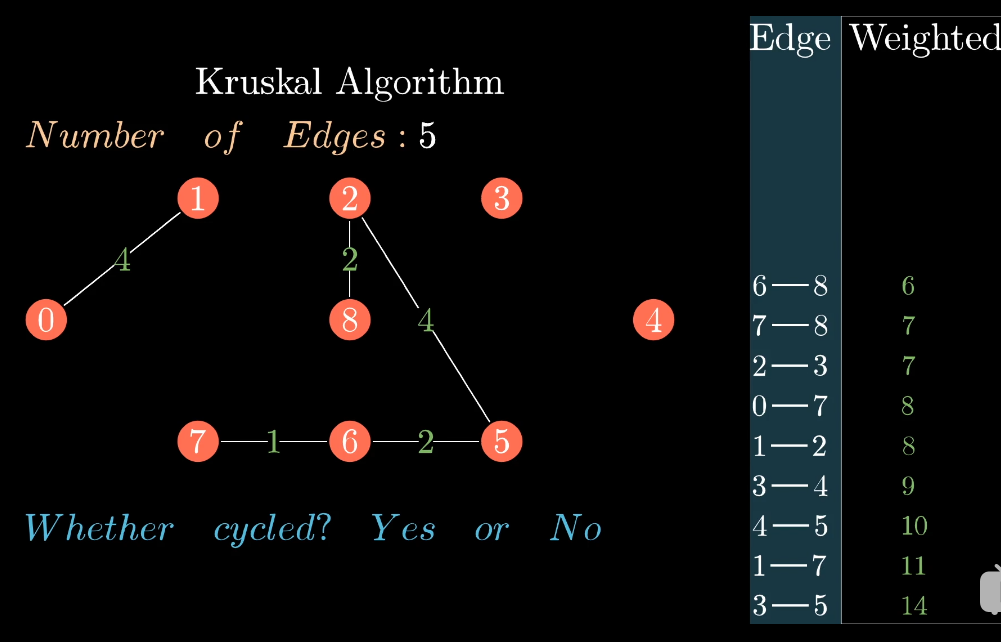
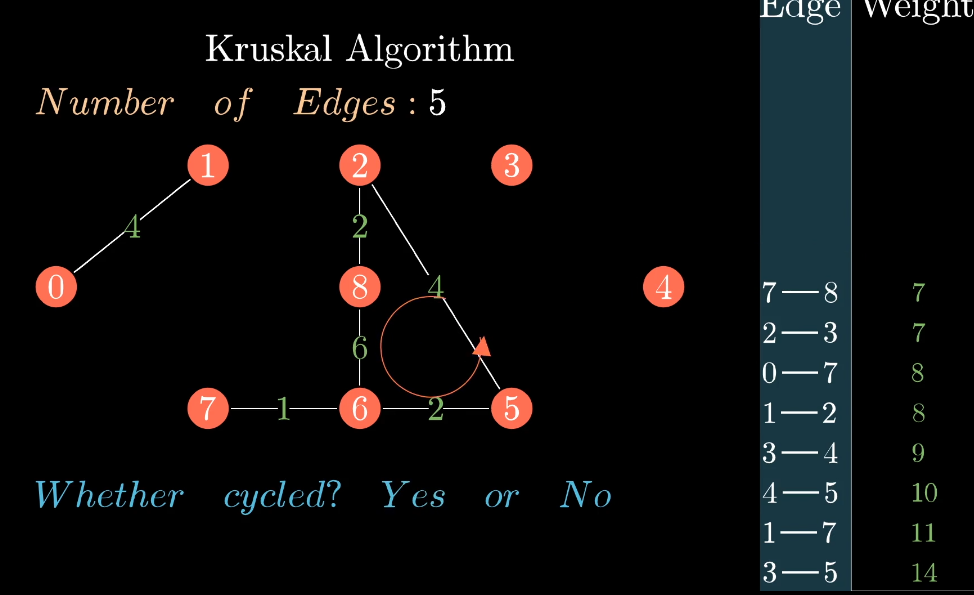
这是又枚举到了6-8这一条边,此时总集合边的数量为5,因为6和8属于同一个集合,加入6-8这条边之后,集合中会构成环,所以将6-8这条边舍弃
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=200010,M=100010;
int p[M];
int n,m;
struct Edge
{
int a,b,w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[N];
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
else return x;
}
int Kruskal()
{
int res=0,cnt=0;//res记录最小生成树的树边权重之和,cnt记录的是全部加入到树的集合中边的数量(可能有多个集合)
for(int i=0;i<m;i++)
{
int a=edges[i].a,b=edges[i].b,w=edges[i].w;
if(find(a)!=find(b))
/*
具体可以参考连通块中点的数量,如果a和b已经在一个集合当中了,说明这两个点已经被一种方式连接起来了,
如果加入a-b这条边,会导致集合中有环的生成,而树中不允许有环生成,所以一个连通块中的点的数量假设
为x,那么里面x个节点应该是被串联起来的,有x-1条边,所以只有当a,b所属的集合不同时,才能将a-b这条
边加入到总集合当中去
*/
{
p[find(a)]=p[find(b)];//将a,b所在的两个集合连接起来
cnt++;//因为加入的是a-b的这一条边,将a,b所在的两个集合连接之后,全部集合中的边数加1
res+=w;//加入到集合中的边的权重之和
}
}
if(cnt==n-1) return res;//可以生成最小生成树
else return 0x3f3f3f3f;//树中有n个节点便有n-1条边,如果cnt不等于n-1的话,说明无法生成有n个节点的树
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++) p[i]=i;//初始化并查集
for(int i=0;i<m;i++)
{
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
edges[i]={a,b,w};
}
sort(edges,edges+m);//将边的权重按照大小一一排序
int t=Kruskal();
if(t==0x3f3f3f3f) printf("impossible\n");
else printf("%d\n",t);
return 0;
}


找根节点不是应该return p[x]吗,x不会改变吧
为什么并查集初始化时要从零开始,n-1结束,不应该是1–n吗
这个应该无所谓的,因为你p[0]是用不到的,到n-1结束那么p[n]=0和前面p[1]到p[n-1]不一样就行
bool operator< (const Edge &W)const
{
return w < W.w;
}
这是啥意思呢
重载小于号,因为在给边排序的时候是按照边的权重进行排序的,这样当两个边进行比较的时候就会使用它们的权重进行比较了
谢谢了
(๑′ᴗ‵๑)I Lᵒᵛᵉᵧₒᵤ❤
为什么要用结构体存储边?
你的N和M在const定义的时候写反了,调半天调不出来
o( ̄┰ ̄*)ゞ不好意思
orz
太优雅了大佬,谢谢你
orz
orz
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
else return x;
}
这个else应该去掉吧, 还有return的应该是p[x], 而且不知道为什么这个函数能返回数值, 这应该递归不了才对, 在自己的编译器就编译不了
int find(int x)
{
if(p[x]!=x) return p[x]=find(p[x]);
return x;
}
else加不加不影响
要是加了话回溯时返回形参, 而且部分旧编译器执行不了。if里面加return也可以执行,但是文章里面只是if else 按理说不对
此时的p[x]=x 所以你返回p[x]和返回x是同一个意思的
这只是要找祖宗节点,没有要求路径压缩
不影响是因为你if后面多加了个return,原文没有很影响
视频很给力!!!
# orz
### Or2
好翘哦
不是只会生成一个最小生成树吗?为啥会可能有多个集合?不应该只能存在一个集合(树)吗?
本文的第一张图就是 多个集合,此时还未连成一棵树,如果没有剩下 的边的话。
博弈论也是你!!!大佬
啊!刚刚回顾并查集那里看到你的题解,现在又看到了你的题解,大佬!受小弟一拜!
for(int i=0;i<n;i++) p[i]=i;//初始化并查集
为什么不是1—n,不是最小从1开始的吗
都可以的
棒,大神
这个地方大神 p[find(a)]=p[find(b)];//将a,b所在的两个集合连接起来,刚开始看的时候,有点蒙,在想大神是不是写错了,因为以前写的时候我都写成p[find(a)]=find(b); 不过后来想了想好像明白了,
假设x=find(b)//找到b的根节点
那么p[x]=x;
所以p[find(b)] =p[x]=x=find(b);
嘿嘿 自己胡乱想的,不知道对不对!
是对的hh
既然他们都是相等的话 直接写find(b)也是可以的吧
可以滴
这个图是用什么软件做的?能讲一下吗
那图怕不是在b站视频里截的
自信点,还有小电视呢
自信点,把怕不是去掉