题目描述

在远古的神秘土地上，有一片神奇的区域（可以视为二维平面），其中分布着许多神秘的魔力点。

小度是一个远近闻名的魔术师，他的魔法水平可以用一个整数$M$表示。

当小度在区域中的某个位置施法时，若一个魔力点与小度的欧几里得距离的平方不超过$M$,则这个魔力点可以为小度提供魔力。

目前区域内有$n$个魔力点，接下来$m$天每天都会发生一个事件，事件可以分成两类：
$add x y：$在坐标$(x,y)$出现了一个新的魔力点。
$query x y：$小度在坐标$(x,y)$施法。

小度希望每次施法的时候，所有存在的魔力点都能为他提供魔力。但是他目前的魔术水平不一定能够做到。

小度希望知道他的魔法水平$M$至少要达到多少，才能做到每次施法都能让所有存在的魔力点为他提供魔力。

输入格式：

第一行包含两个正整数 $n$ 和 $(1≤ n,m ≤10^5 )$, 分别表示初始点集合的大小和天数；
接下来$n$行，每行包含两个整数$x$和$y$ $(−10^9 ≤ x,y ≤ 10^9 )$，表示集合中的一个魔力点的横坐标和纵坐标；
再接下来$m$行，每行描述一个操作。
操作描述以字符串$s$开头，若$s$为$”add”$，表示添加点操作，后跟两个整数$x$和$y$ $(−10^9≤x,y≤10^9)$，表示要添加的魔力点的横坐标和纵坐标；若$s$为$”query”$，表示查询点操作（施法），后跟两个整数$x$和$y$ $(−10^9 ≤x,y≤10^9)$，表示需要查询的点的横坐标和纵坐标。

输出格式：

一行包含一个整数，输出答案。

输入：

5 3
0 0
3 4
1 1
-2 7
6 -8
query 2 3
add 5 -5
query 0 0

输出：

137

题目分析

凸包+闵可夫斯基和+分治

题目还是有难度的
先说一下做题历程吧

刚开始肯定是暴力，纯暴力$O(n * m)$，当然也只过了4个点

C++ 代码

#include<bits/stdc++.h> 
#define int long long
#define x first
#define y second

using namespace std;
typedef pair<int , int> PII;
const int N = 200010;
int n , m , idx ;
string s;
PII q[N];

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0) , cout.tie(0);
    cin >> n >> m;
    idx = n;
    for(int i = 0 ; i < n ; i ++)
        cin >> q[i].x >> q[i].y;

    sort(q , q + n , [&](PII a , PII b){
        return a.x * a.x + a.y * a.y < b.x * b.x + b.y * b.y;
    });
    int a , b;
    int ans;
    while(m --)
    {
        cin >> s >> a >> b;
        if(s == "add")
        {
            q[idx ++] = {a , b};
            sort(q , q + idx , [&](PII a , PII b){
            return a.x * a.x + a.y * a.y < b.x * b.x + b.y * b.y;
            });
        }
        else 
        {
            auto t = q[idx - 1] , k = q[0];
            ans = max(ans , max((t.x - a) * (t.x - a) + (t.y - b) * (t.y - b) , (k.x - a) * (k.x - a) + (k.y - b) * (k.y - b)));
        }
    }
    cout << ans << '\n';
    return 0;
}

下面来讲讲看了题解的思路

从上面的暴力可以看出，在线做法肯定是行不通的，每次增加和询问都得$O(n)$ 肯定是会爆掉的
所以采用离线做法

首先看题目很好理解，就是就点集的最长距离，再细一点，点集一共有两种，一种是原来就给定的$n$个点的点集，然后就是新增询问中的$m$个点的点集，而且这个点集中还要注意，有的是增点，有的是询问，我们要求的询问的点与再此之前的点集的最远距离

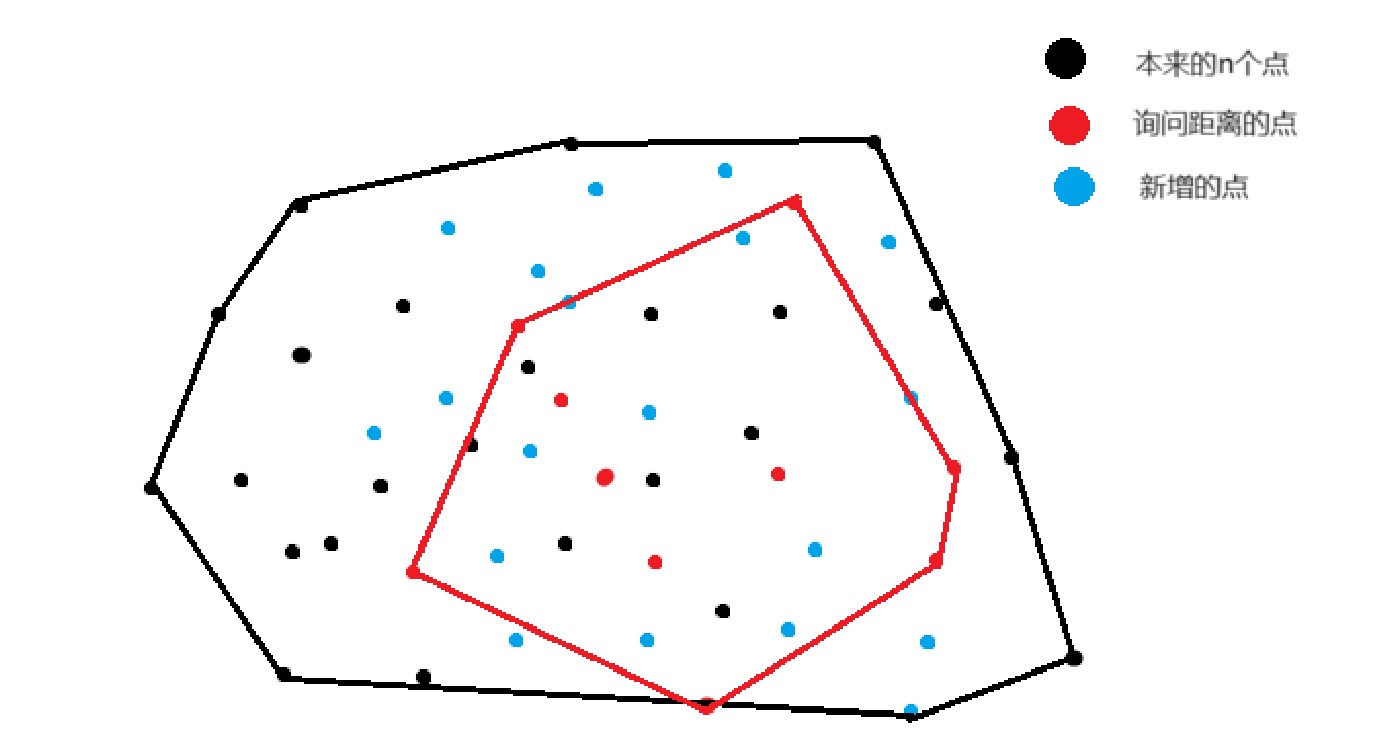
图示如下

要求红点点集与蓝点和黑点点集的最长距离，同时还要注意求的先后顺序，因为只有在询问距离之前新增的点对最长距离有贡献

为了方便，我们先暂且忽略先后贡献的问题，我们先解决点集之间最长距离的事
我们发现。点集之间最长距离一定不会由中间的点决定，那么对于两个点集，我们先求对应凸包

求这两个凸包之间的最长距离，暴力就得$O(n * m)$，肯定不行
那就要把这两个凸包按照某个顺序选择点进行计算，优化成线性复杂度$O(n)$
这个时候我们想到了闵可夫斯基和
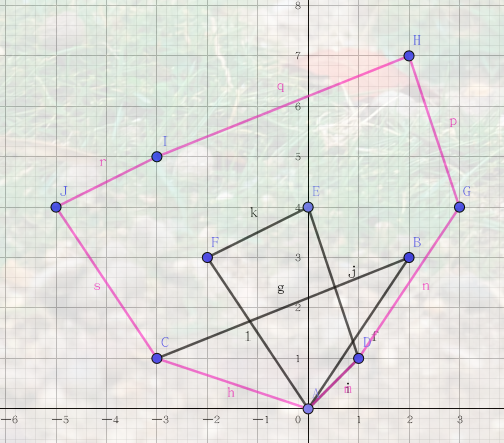
闵可夫斯基和通俗点讲就是将一个图形$A$平移地放在着图形$B$每个顶点上，再将此时图形$A$的顶点标注出来，求出此时的凸包，这就是闵可夫斯基和了
根据对称性，$A$放$B$上和$B$放$A$上构成的凸包应该是相同的，所以闵可夫斯基和是唯一的
举个三角形和四边形的闵可夫斯基和的例子（图是盗的）

再仔细看看图形，会感觉好像跟题目要求的距离没啥关系
题目要求两个点集之间的最远距离
形象一点 有两个点$P(x1 , y1)$和$Q(x2 , y2)$
那我们就要求 $P - Q = (x1 - x2 , y1 - y2)$ 向量的模长最大值
欸，等一下，向量模长最大值，每个向量对应一条边，如果这些向量能构成凸包就好了，这样就能和求出来的闵可夫斯基和挂上钩了
再想想，怎么才能求出这样的闵可夫斯基和呢，其实把点$Q$所在点集都换成和$-Q$值一样的点不就行了，这样求出来的闵可夫斯基和每条边就和要求的向量对应了
这样就可以转化成求闵可夫斯基和凸包边模长的最大值

闵可夫斯基和求法如下：

求凸包之间的闵可夫斯基和的方法。
把两个凸包的每一条向量都抠出来，按照极角序排序构成新凸包即可。
注意点和向量的去重(向量相同斜率去重)。
还有个地方可以提一下：求多个凸包的闵可夫斯基和的时候可以直接全把边拿出来一块求，没有必要两个两个求。
具体实现的时候，找出最高且最靠左的点。
先把这个点加入答案，从这个点开始把所有向量遍历一遍，最后去掉最后一个点即可(最后这个点会和第一个点重合)。

现在求最长距离的事情解决了，还有个事就是得考虑下时间的问题，本来想的kd树或时间序列啥的，但其实很简单

分治就行了
神奇吧
仔细想想，对于询问距离的所有点来说，只有在它之前的点对其距离的最大值有贡献，那我们就分成前半段和后半段
前半段的存在的点和所有新增的点都可以对后半段的询问距离做出贡献，那我们就求前半段存在的点和所有新增的点（蓝+黑）所构成的点集和后半段询问距离的点（红）构成的点集求闵可夫斯基和，然后继续递归分治即可

最后给下代码 但是还是有一个点被卡

C++代码 (34/35) 时间复杂度$O(nlog^2(n))$

#include<bits/stdc++.h> 
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int , int> PII;
const int N = 200010;
PII q[N];
int n , m , op[N] ;
int ans;
PII operator+(PII a ,PII b)
{
    return {a.x + b.x , a.y + b.y};
}

PII operator-(PII a , PII b)
{
    return {a.x - b.x , a.y - b.y};
}

int operator*(PII a , PII b)
{
    return a.x * b.y - a.y *b.x;
}

int operator&(PII a , PII b)
{
    return a.x * b.x + a.y *b.y;
}

vector<PII> andrew(vector<PII> q)
{
    for(auto &i : q)
        if(i.x == q[0].x && i.y < q[0].y  || i.x < q[0].x) swap(i , q[0]);

    sort(q.begin() + 1 , q.end() , [&](PII a , PII b){
        return ((a - q[0]) * (b - q[0])) > 0;
    });
    vector<PII> ans;
    for(auto i : q)
    {
        while(ans.size() >= 2 && (i - ans.back()) * (ans.back() - ans[ans.size() - 2]) >= 0 )
        {
            ans.pop_back();
        } 
        ans.push_back(i);
    }
    return ans;
}

int cmp(PII a , PII b)
{
    if((a.x > 0 || a.x == 0 && a.y > 0) != (b.x > 0 || b.x == 0 && b.y > 0)) return (a.x > 0 || a.x == 0 && a.y > 0);
    return a * b > 0;
}

void Mincowsky_sum(vector<PII> a , vector<PII> b) // 闵可夫斯基和
{
    if(a.empty() || b.empty()) return;
    a = andrew(a) , b = andrew(b);

    vector<PII> c , ca , cb;
    if(a.size() > 1)
    {
        a.push_back(a.front());
        for(int i = 1 ; i < a.size() ; i ++) ca.push_back(a[i] - a[i - 1]);
    }
    if(b.size() > 1)
    {
        b.push_back(b.front());
        for(int i = 1 ; i < b.size() ; i ++) cb.push_back(b[i] - b[i - 1]);
    }
    c.resize(ca.size() + cb.size());
    merge(ca.begin() , ca.end() , cb.begin() , cb.end() , c.begin() , cmp);
    PII cur = a[0] + b[0];
    ans = max(ans , (cur & cur));
    for(auto i : c)
        cur = cur + i , ans = max(ans ,(cur & cur));
}

void calc(int l , int r) // 分治
{
    if(l == r) return;
    int mid = l + r >> 1;
    vector<PII> L , R;
    for(int i = l ; i <= mid ; i ++) if(op[i] == 1) L.push_back(q[i]);
    for(int i = mid + 1 ; i <= r ; i ++) if(op[i] == 2) R.push_back(q[i]);
    Mincowsky_sum(L , R);
    calc(l , mid) , calc(mid + 1 , r);
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0) , cout.tie(0);
    cin >> n >> m;
    for(int i = 1 ; i <= n ; i ++) cin >> q[i].x >> q[i].y , op[i] = 1;
    for(int i = n + 1 ; i <= n + m ; i ++)
    {
        string s;
        cin >> s >> q[i].x >> q[i].y;
        if(s == "add") op[i] = 1;
        else op[i] = 2 , q[i].x = -q[i].x , q[i].y = -q[i].y;
    }
    calc(1 , n + m);
    cout << ans << '\n';
    return 0;
}