题目描述
有$n$ 支队伍参加一项赛事,其中$n=2^k ,k∈N$ ,给这些队伍从 $1$ 到 $n $编号。
该赛事采用淘汰赛制,经过$k$ 轮共$2^k − 1$ 场淘汰赛决出最后的冠军。具体规则如下:
- 第 $1$ 轮比赛有 $2^k − 1$ 场,分别是$1$号队伍对阵$2$号队伍,$3$ 号队伍对阵$4$ 号队伍,$5$ 号队伍对阵 $6$ 号队伍,......... ,$2^k − 1$ 号队伍对阵$2^k$ 号队伍。
- 对于所有 $2 \le t \le k $,第$t$ 轮比赛有$2^{k−t}$ 场,分别是第$t−1$ 轮第$1$场的胜者对阵第$t−1$ 轮第$2$ 场的胜者,第$t−1$ 轮第$3$ 场的胜者对阵第$t−1$ 轮第$4$ 场的胜者,第$t−1$ 轮第$5$场的胜者对阵第$t−1$ 轮第$6$ 场的胜者,…,第$t−1$ 轮第$2^{k−t+1} − 1$ 场的胜者对阵第$t−1$ 轮第$2^{k−t+1}$ 场的胜者。
某公司给出一个竞猜规则:如果在第$i$支队伍身上下$x$的赌注,则该队伍每参加一场比赛,返还$x$元,如果该队伍最终夺冠,则额外奖励 $a_ix$ 元,其中$a_i$ 为该公司在整届赛事开始前给出的夺冠赔率。
现有一个赌怪想要参加竞猜,他一开始打算给第$i$ 支队伍下$b_i$ 赌注。他会进行$q$ 次操作,每次操作给定$id$ 和$d$,表示将$b_{id}$ 改为$b_{id} + d$,然后询问他至少可以获得多少回报。
输入格式:
第 $1$ 行输入 $1$ 个正整数$n(n=2^k ,1 \le k \le 20)$,表示有$n$ 支队伍参加该项赛事;
第 $2$ 行输入$n$ 个正整数$a_i (1 \le a_i \le 100)$,分别表示第$i$ 支队伍的夺冠赔率;
第 $3$ 行输入$n$ 个非负整数 $b_i (0 \le b_i \le 10^5)$ ,分别表示一开始赌怪在第$i$ 支队伍身上下的赌注;
第 $4$ 行输入$1$ 个整数$q(1 \le q \le 5×10^5)$,表示共有$q$ 次操作;
接下来共有$q$ 行,每行输入$2$ 个数,其中的第$i$ 行输入两个整数$id_i(1 \le id_i \le n)$ 和$d_i (−100 \le d_i
\le 100)$,表示将$b_{id_i}$ 修改为 $b_{id_i} + d_i$ 保证任意修改后$0 \le b_{id_i} \le 10^5$
输出格式:
$q$ 行,每行输出一个整数,第 $i$ 行输出第$i$次操作后赌怪至少可以获得的回报。
样例1
输入:
2
1 6
7 2
1
2 7
输出:
23
样例 2
输入:
4
8 3 5 1
7 5 9 9
2
1 8
4 -2
输出:
61
55
题目分析
线段树+贪心
首先画一颗比赛树
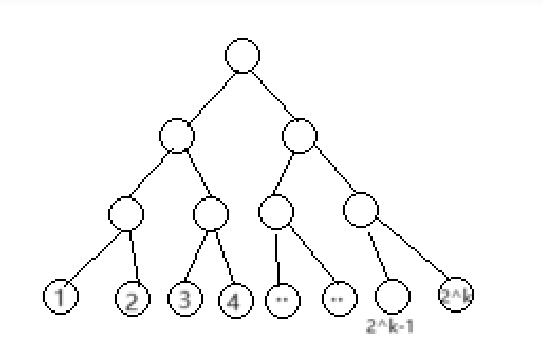
我们要计算所有比赛队伍能够带来的最小收益(因为问的是至少)
再观察题目,可以知道夺冠队伍对总收益的贡献和非夺冠队伍的贡献不一样
对于非夺冠队伍贡献值的计算,只要沿着它获胜的路径累加一遍即可
这样一来,我们可以发现,其计算的本质有点像DFS,但是深搜一遍肯定会TLE,又所有的节点操作又是一样的,我们不难想到线段树这种数据结构
那么节点又应该有什么性质呢?
首先应该有$l,r$ 线段树基本性质
然后应该去维护一下这个节点是哪个子节点能够胜利,看哪个子节点的价值小就行
最后还要看这个节点对总收益的贡献,而且注意,获胜和未获胜的贡献还是不一样的
struct TreeNode
{
int l , r;
LL val;
LL w[2]; // w[1] 表示夺冠的贡献 w[0] 表示非夺冠的贡献
};
现在考虑维护信息
初始建树的时候
对于子节点$val$和$w[0]$是一样的应该都是他们所对应的赌注
$w[1]$不同,看题目,获胜的队伍获胜的时候会获得$a_ix$的奖励所以对于叶子节点,如果是获胜队伍的话贡献应该是本身的赌注乘以到根节点儿子的深度再加上本身夫人赌注乘以夺冠倍率
对于更新父节点信息
本身的节点胜利的是谁,价值就是哪个子节点的价值,根据贪心,我们要选择价值小的子节点
tr[u].val = min(tr[u << 1].val , tr[u << 1 | 1].val);
然后是计算贡献
如果未夺冠,那么该节点的总贡献就是本身胜利的队伍赌注加上两个子节点的总贡献,因为是未获胜,所以加上的自然也是子节点的未获胜状态的贡献
tr[u].w[0] = tr[u << 1].w[0] + tr[u << 1 | 1].w[0] + tr[u].val;
如果夺冠,那么该节点的总贡献就会不同,首先本身胜利的队伍就是夺冠的队伍,之前给子节点赋值的时候讨论过,获胜叶子节点的贡献值是直接计算到根的,不需要再计算一遍,所以不需要再加一遍节点的本身价值,现在就只需要考虑子节点到父节点贡献值的状态转移了
夺冠的只能有一个子节点,另一个子节点必须未获胜,所以一共就两种情况,贪心取最小即可
tr[u].w[1] = min(tr[u << 1].w[0] + tr[u << 1 | 1].w[1] , tr[u << 1].w[1] + tr[u << 1 | 1].w[0]);
剩下的就简单了,修改就是板子中再简单不过的单点查询,总贡献的最小值就是根节点的贡献值,注意,根节点必须获胜(不然哪来的冠军),代码如下
C++ 代码 MLE(10/20)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = (1 << 20) + 10;
int n , k ;
int a[N] , b[N];
struct TreeNode
{
int l , r;
LL val;
LL w[2]; // w[1] 表示夺冠的贡献 w[0] 表示非夺冠的贡献
}tr[N * 4];
void pushup(int u)
{
tr[u].val = min(tr[u << 1].val , tr[u << 1 | 1].val);
tr[u].w[0] = tr[u << 1].w[0] + tr[u << 1 | 1].w[0] + tr[u].val;
tr[u].w[1] = min(tr[u << 1].w[0] + tr[u << 1 | 1].w[1] , tr[u << 1].w[1] + tr[u << 1 | 1].w[0]);
}
void build(int u , int l , int r)
{
tr[u].l = l , tr[u].r = r;
if(l == r)
{
tr[u].w[0] = tr[u].val = b[l];
tr[u].w[1] = (k - 1 + a[l]) * b[l];
return;
}
int mid = l + r >> 1;
build(u << 1 , l , mid);
build(u << 1 | 1 , mid + 1 , r);
pushup(u);
}
void modify(int u , int id , int d)
{
if(tr[u].l == id && tr[u].r == id) // 找到了
{
tr[u].val += d;
tr[u].w[0] += d;
tr[u].w[1] += (k - 1 + a[tr[u].l]) * d;
b[tr[u].l] += d;
return;
}
int mid = tr[u].l + tr[u].r >> 1;
if(id <= mid) modify(u << 1 , id , d);
else modify(u << 1 | 1 , id , d);
pushup(u);
}
int main( )
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
cin >> n;
while(1 << k != n) k ++;
k ++;
for(int i = 1 ; i <= n ; i ++) cin >> a[i];
for(int i = 1 ; i <= n ; i ++) cin >> b[i];
build(1 , 1 , n);
int q;
cin >> q;
while(q --)
{
int id , d;
cin >> id >> d;
modify(1 , id , d);
cout << tr[1].w[1] << '\n';
}
return 0;
}
交完后发现$MLE$了,算一下,结构体中两个$int$,两个$long long$ ,就是$24$字节,$2^{20} * 4 * 24 \approx 2^{25} $
题目是$64MB$ 就是$64 * 1024 * 1024 = 2^{26}$ 很接近,所以爆了
所以需要将节点中的$l , r$ 优化掉,因为只在查询中用过$l , r$,所以我们直接折半查询,缩短查询范围而不是通过节点本身的$l , r$来确定查询范围
代码如下
C++ 代码 AC(20/20)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = (1 << 20) + 10;
int n , k ;
int a[N] , b[N];
struct TreeNode
{
LL val;
LL w[2]; // w[1] 表示夺冠的贡献 w[0] 表示非夺冠的贡献
}tr[N * 4];
void pushup(int u)
{
tr[u].val = min(tr[u << 1].val , tr[u << 1 | 1].val);
tr[u].w[0] = tr[u << 1].w[0] + tr[u << 1 | 1].w[0] + tr[u].val;
tr[u].w[1] = min(tr[u << 1].w[0] + tr[u << 1 | 1].w[1] , tr[u << 1].w[1] + tr[u << 1 | 1].w[0]);
}
void build(int u , int l , int r)
{
if(l == r)
{
tr[u].w[0] = tr[u].val = b[l];
tr[u].w[1] = (k - 1 + a[l]) * b[l];
return;
}
int mid = l + r >> 1;
build(u << 1 , l , mid);
build(u << 1 | 1 , mid + 1 , r);
pushup(u);
}
void modify(int u , int l , int r , int id , int d)
{
if(l == id && r == id) // 找到了
{
tr[u].val += d;
tr[u].w[0] += d;
tr[u].w[1] += (k - 1 + a[l]) * d;
b[l] += d;
return;
}
int mid = l + r >> 1;
if(id <= mid) modify(u << 1 , l , mid , id , d);
else modify(u << 1 | 1 , mid + 1 , r , id , d);
pushup(u);
}
int main( )
{
ios::sync_with_stdio(false);
cin.tie(0) , cout.tie(0);
cin >> n;
while(1 << k != n) k ++;
k ++;
for(int i = 1 ; i <= n ; i ++) cin >> a[i];
for(int i = 1 ; i <= n ; i ++) cin >> b[i];
build(1 , 1 , n);
int q;
cin >> q;
while(q --)
{
int id , d;
cin >> id >> d;
modify(1 , 1 , n , id , d);
cout << tr[1].w[1] << '\n';
}
return 0;
}

