题目描述

为了原画集，小度在努力地凹深渊。
深渊共有$n$波怪物，其中第$i$波怪物由$m_i$只生命值为$a_i$的怪物组成。一开始场上只有第$1$波的怪物，当第$i$波怪物被全部击败时，第$i+1$ 波怪物会立即出现在场上。当第$n$波怪物被全部击败时，游戏结束。由于小度操作不行，当开始攻击一个怪物时，在该怪物被击败前，不能更换攻击目标。
小度拿出了他仅用了$6$ 抽就抽到的希儿来打深渊，希儿共有两种攻击方式：
1. 普通攻击，对$1$个怪物造成$1$点伤害，消耗$1$秒的时间；
2.必杀技，对$1$个怪物造成$k$点伤害，不消耗时间。

其中普通攻击在任意时刻都是可用的；必杀技在初始时是可用的，每次使用必杀技后，必杀技会进入不可用状态，当希儿用除必杀技以外的攻击击败怪物时，必杀技会进入可用状态。

小度想要尽可能高的分数，也就是说希望用尽可能短的时间结束游戏，现在请你帮小度计算，至少要多少时间才可以结束游戏。

输入格式：

第$1$行$2$个正整数$n$ $(1 \le n \le 10^5)$和$k (2 \le k \le 10^5)$，表示共有$n$波怪物，必杀技可以造成$k$点伤害；

接下来共$n$ 行，每行两个正整数$a_i (1 \le a_i \le 10^5)$和$m_i (1 \le m_i \le 10^5)$，表示第$i$波怪物由$m_i$只生命值为$a_i$的怪物组成。

输出格式：

一行，输出一个整数，表示至少要多少时间才可以结束游戏。

样例 1

输入：

3 2
1 1
2 1
3 1

输出：

3

样例 2

输入：

5 3
2 2
3 1
4 3
1 2
5 2

输出：

13

题目分析

作为一个星批，$6$发出希儿我不是很认可······

线性$dp$ + 贪心

首先贪心地想一下，无论怎样，多使用必杀技一定是最好的，因为必杀技不消耗任何时间
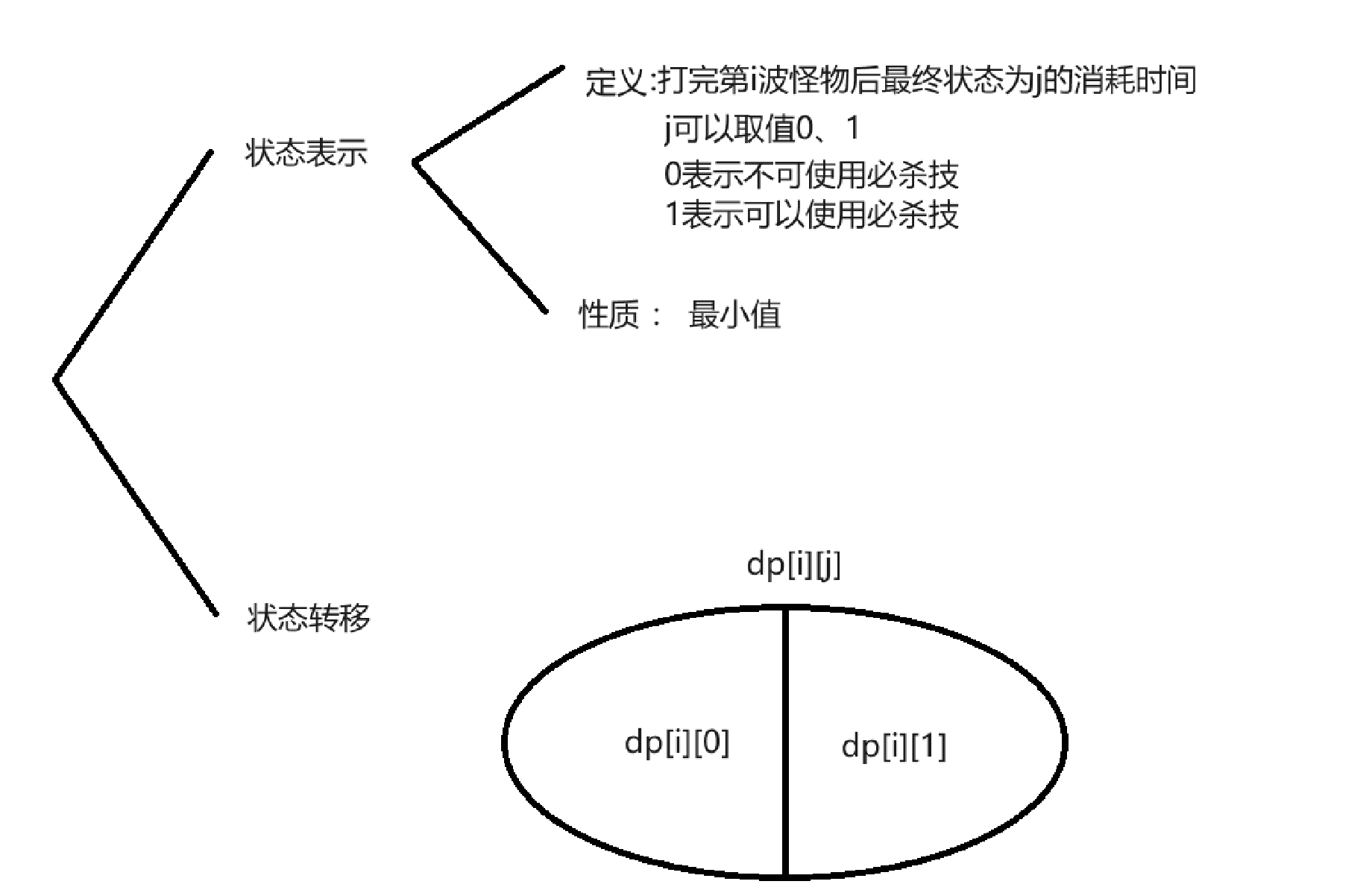
设状态为$j$ ， $j$可以取$0$或$1$，$0$表示不可使用必杀技，$1$表示可以使用必杀技
根据题目，$1$可以转移至$0$或$1$ ，而$0$只能转移至$1$
但是我们贪心地想一下，其实$1$转移至$1$很亏的，好不容易有一次使用必杀技的机会没有用到，时间上肯定会长
所以肯定是能用则用

下面来分析必杀技的使用
如果$k$很大，大到可以秒掉一个怪兽，我们就可以贪心一下，隔一个怪兽使用一次必杀技
1.如果不要留住必杀技的使用

• 如果开始不可使用必杀技，那开始就得必须使用普攻打死共需要 $\lceil \frac{m}{2} \rceil * a$ 次普攻
• 如果开始可以使用必杀技，那开始就不用使用普攻了 ， 共需要$\lfloor \frac{m}{2} \rfloor * a$次普攻

2.如果想要留住必杀技的使用

• 如果开始不可使用必杀技，那开始和最后一个就得必须使用普攻打死共需要 $(\lfloor \frac{m}{2} \rfloor + 1) * a$次普攻
• 如果开始可以使用必杀技，那开始就不用使用普攻了 ， 共需要$\lceil \frac{m}{2} \rceil * a$次普攻

如果$k$不大，不能一招秒掉一个怪兽
那事情就很好办了
首先根据贪心，一定是要使用到必杀技的，那么还想要杀死怪兽，就得加上 $(a - k)$次普攻，每个怪兽都一样，这么看来其实最后是什么状态取决于你放招的顺序，而消耗的最短时间是一样的
还要注意，如果开始不能使用必杀技，就得比使用必杀技多消耗$k$次普攻

$dp$转移如下

C++ 代码 空间$O(n)$

#include<bits/stdc++.h> 
#define int long long
using namespace std;
const int N = 100010;
int n , k;
int a[N] , m[N];
int dp[N][2]; // 1表示可以使用必杀技 、0表示不可以使用必杀技
signed main()
{
    cin >> n >> k;
    for(int i = 1 ; i <= n ; i ++) cin >> a[i] >> m[i];
    for(int i = 1 ; i <= n ; i ++)
    {
        if(k < a[i]) // 不能必杀技直接杀死  
            dp[i][1] = dp[i][0] = min(dp[i - 1][0] + k , dp[i - 1][1]) + m[i] * (a[i] - k);
        else
        {
            dp[i][0] = min(dp[i - 1][0] + (m[i] + 1) / 2 * a[i] , dp[i - 1][1] + m[i] / 2 * a[i]);
            dp[i][1] = min(dp[i - 1][0] + (m[i] / 2 + 1) * a[i] , dp[i - 1][1] + (m[i] + 1) / 2 * a[i]);
        }
    }

    cout << min(dp[n][1] , dp[n][0]) << '\n';

    return 0;
}

仔细看代码可以发现，每一次更新只用到上一次的状态，这里其实可以用滚动数组优化

空间优化 $O(1)$

#include<bits/stdc++.h> 
#define int long long
using namespace std;
int n , k;
int dp[2]; // 0表示可以使用必杀技 、1表示不可以使用必杀技
signed main( )
{
    cin >> n >> k;
    for(int i = 0 ; i < n ; i ++)
    {
        int a , m;
        cin >> a >> m;
        if(k < a) // 不能必杀技直接杀死  
            dp[1] = dp[0] = min(dp[0] + k , dp[1]) + m * (a - k);
        else
        {
            int dp0 = min(dp[0] + (m + 1) / 2 * a , dp[1] + m / 2 * a);
            int dp1 = min(dp[0] + (m / 2 + 1) * a , dp[1] + (m + 1) / 2 * a);
            dp[0] = dp0 , dp[1] = dp1;
        }
    }

    cout << min(dp[1] , dp[0]) << '\n';

    return 0;
}