为了提升自己,重新整理提高课,把每一种题型的题都重新写一遍,然后写成题解,如果有错误还请劳烦您指正,多谢
2023/9/25 第3题
题目描述
设有 N×N 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
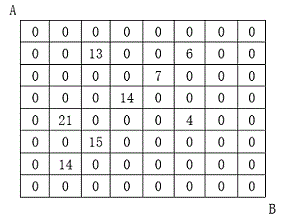
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
输入格式
第一行为一个整数N,表示 N×N 的方格图。接下来的每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数行和列编号从 1 开始。一行“0 0 0”表示结束。
输出格式
输出一个整数,表示两条路径上取得的最大的和。
数据范围
N≤10
样例
输入样例:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例:
67
算法
(线性动态规划) O(n3)
这道题在连个月前难到我怀疑人生,总是想不明白为什么这么做
两个月后,我简简单单做完了这个题没有一点感觉
所以,努力就不会辜负自己,加油…跑题了,回来
这道题和上面两道题最大的区别就是,有两条道,而且还会取走这个数,说明不能走同一条道,如果进行两次单路径动态规划的话,还要回溯标记取走点,太过麻烦而且很容易出错,因此我们直接考虑两条线路同时进行,保证两条线路同时进行而且互相不打扰的前提条件是:最终的终点相同。
这个条件看起来不起眼,但是深究另藏玄🐔,这个条件非常重要,它代表着两条路径走过的点的数量是相同的,这就是平衡两条路径的最好的选择
所以我们动态规划时使用三重数组,第一重用于稳定大局,相当于元帅,统领后面两条路径,用 k 表示,k表示当前走了多少步了,相当于当前格子的行和列加起来的值,定住了k,另外两条路的活动范围就定住了。
另外两重数组表示当前 k 步下,每一条路当前的横坐标,知道了横坐标,纵坐标就可以用 k 减去横坐标得到
注意一点,当前的格子如果被遍历到了,是会被拿走的,所以当两条路走了同一个格子时,即i1 == i2,当前的转移方程只能加上一次这个值
开搞!
闫氏DP分析法:
动态规划:
状态表示:
表达式:f[k][i1][i2]
含义:走了 k 步,第一条路走到i1行,第二条路走到i2行时的最大值
状态计算:
&x = f[k][i1][i2];
t 表示两条路径在当前两个格子上取到的数的和
1. 第一条路上一行 和 第二条路上一列 x = max(x,f[k-1][i1-1][i2]) + t;
2. 第一条路上一行 和 第二条路上一行 x = max(x,f[k-1][i1-1][i2-1]) + t;
3. 第一条路上一列 和 第二条路上一列 x = max(x,f[k-1][i1][i2]) + t;
4. 第一条路上一列 和 第二条路上一行 x = max(x,f[k-1][i1][i2-1]) + t;
参考文献
算法提高课
C++ 代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 15;
int n;
int g[N][N];
int f[2*N][N][N];
int main()
{
cin>>n;
int a,b,c;
while(cin>>a>>b>>c,a||b||c)
{
g[a][b] = c;
}
for(int k = 2;k<=n*2;k++)
{
for(int i1 = 1;i1 <= k;i1++)
{
for(int i2 = 1;i2<=k;i2++)
{
int j1 = k-i1,j2 = k-i2;
int &x = f[k][i1][i2];
int t = g[i1][j1] + g[i2][j2];
if(j1 == j2) t /= 2;
x = max(x,f[k-1][i1][i2]+t);
x = max(x,f[k-1][i1-1][i2]+t);
x = max(x,f[k-1][i1][i2-1]+t);
x = max(x,f[k-1][i1-1][i2-1]+t);
}
}
}
cout<<f[2*n][n][n]<<endl;
return 0;
}
今天的回忆就到这里,先去刷个洛谷先

