宣传一下 算法提高课整理

CSDN个人主页：更好的阅读体验

原题链接

题目描述

给定长度为 $N$ 的数列 $a$，以及 $M$ 条指令，每条指令可能是以下两种之一：

1. 1 x y，查询区间 $[x,y]$ 中的最大连续子段和，即

$$\max\limits_{x \le l \le r \le y} (\sum\limits^r_{i=l} a_i)$$

1. 2 x y，把 $a_x$ 改成 $y$。

对于每个查询指令，输出一个整数表示答案。

输入格式

第一行两个整数 $N,M$。

第二行 $N$ 个整数 $a_i$。

接下来 $M$ 行每行 $3$ 个整数 $k,x,y$，$k=1$ 表示查询（此时如果 $x>y$，请交换 $x,y$），$k=2$ 表示修改。

输出格式

对于每个查询指令输出一个整数表示答案。

每个答案占一行。

数据范围

$N \le 500000, M \le 100000$,
$-1000 \le a_i \le 1000$

输入样例：

5 3
1 2 -3 4 5
1 2 3
2 2 -1
1 3 2

输出样例：

2

思路

要求一段区间的最大连续子段和，我们思考要维护哪些信息。

区间 $[x,y]$ 的最大和子段 $[l,r]$ 有 $4$ 种情况：

1. $x<l<r<y$
   
   此时将这段区间放在线段树中，

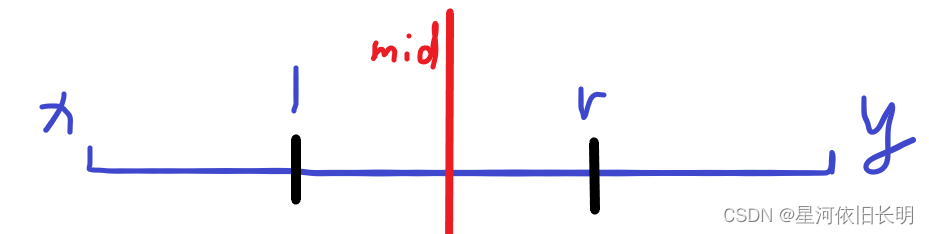
我们发现，应该维护每个区间的 最大前缀和 和 最大后缀和。

1. $x=l<r<y$

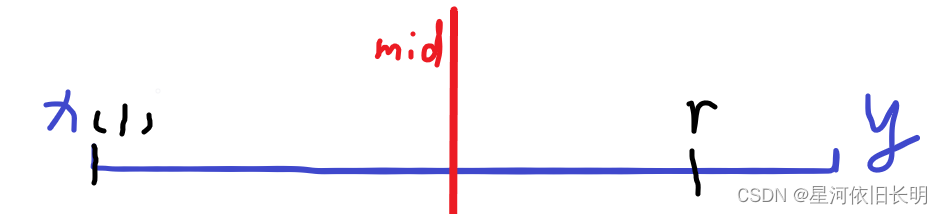
此时我们发现还应该维护每个区间的 总和 。

1. $x<l<r=y$
   
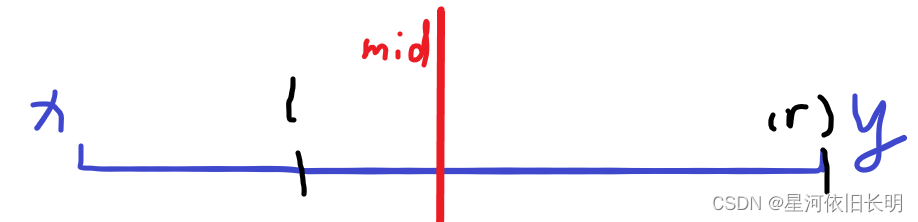
   此情况与“2”同理。

2. $x=l<r=y$

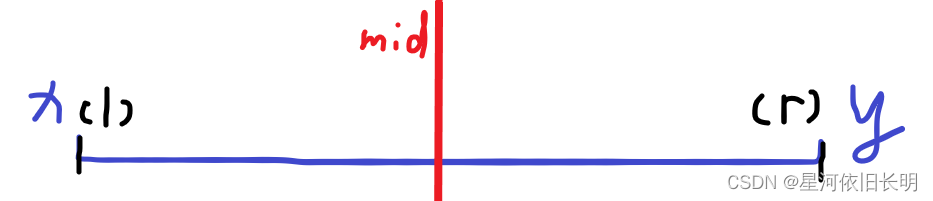
同理。

所以我们维护四个值：总和、最大子段和、最大前缀和、最大后缀和。

• 初始状态（区间只有一个元素）：这四个值都是元素值。
• 上传：
  • 显然，总和直接加起来即可。
  • 最大前缀和为 $\max ($左儿子最大前缀和，左儿子区间和+右儿子最大前缀和$)$。
  • 最大后缀和为 $\max ($右儿子最大后缀和，右儿子区间和+左儿子最大后缀和$)$。
  • 最大子段和为 $\max ($左儿子最大子段和，右儿子最大子段和，左儿子最大后缀和+右儿子最大前缀和$)$。
• 单点修改：与初始状态的设定相同。
• 区间查询：由于要用到叶子节点的多个值，我们选择以结构体作为返回值。在获取了左右儿子的返回值之后建立一个新节点 res 并将返回值上传至 res 。
• 输出：输出返回值的最大子段和即可。
• 注意：可能有 $x>y$，所以特判一下。

算法时间复杂度

线段树单点修改区间查询， $O(n \log n)$ 。

AC Code

$\text{C}++$

#include <iostream>

using namespace std;

const int N = 500010;

struct Segment_Tree_Node
{
    int l, r;
    int sum, tmax; // 总和、最大子段和
    int lmax, rmax; // 最大前缀、最大后缀
}tr[N * 4];

int n, m;
int w[N];

void PushUp(Segment_Tree_Node &p, Segment_Tree_Node &l, Segment_Tree_Node &r)
{
    p.sum = l.sum + r.sum;
    p.lmax = max(l.lmax, l.sum + r.lmax);
    p.rmax = max(r.rmax, r.sum + l.rmax);
    p.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[l], w[l], w[l], w[l]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        PushUp(tr[u], tr[u << 1], tr[u << 1 | 1]);
    }
}

void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v};
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        PushUp(tr[u], tr[u << 1], tr[u << 1 | 1]);
    }
}

Segment_Tree_Node query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return query(u << 1, l, r);
        else if (l > mid) return query(u << 1 | 1, l, r);
        else
        {
            Segment_Tree_Node L = query(u << 1, l, r);
            Segment_Tree_Node R = query(u << 1 | 1, l, r);
            Segment_Tree_Node res;
            PushUp(res, L, R);
            return res;
        }
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ )
    scanf("%d", &w[i]);

    build(1, 1, n);

    int k, x, y;
    while (m -- )
    {
        scanf("%d%d%d", &k, &x, &y);
        if (k == 1) printf("%d\n", query(1, min(x, y), max(x, y)).tmax);
        else modify(1, x, y);
    }

    return 0;
}

最后，如果觉得对您有帮助的话，点个赞再走吧！