题目描述
现在小度在石碑上找到了一些文字,这些文字包含$N$个英文字符,这些文字依稀可以辨认出来,另一些文字难以辨认,在可以辨认出来的文字中,小度发现了他喜欢的文字$shs$,小度习惯把喜欢的事物说三遍及以上,他希望知道原始的石碑上有多少种可能性会出现三次及以上$shs$(三个$shs$不能出现重合,即$shshs$只能算出现一次$shs$),这样的碑文可能有很多,你只需要输出答案对1e9+7取模的结果即可。
输入格式
一行输入的是整数 $n$ $(1 \leq n \leq 10^6)$
),表示碑文长度 。
输出格式
一行一个数字,表示有多少种字符串可能出现了三个及以上$shs$。
样例输入
10
样例输出
104
题目分析
首先我们发现此题需要3个$shs$串才能达到计数标准,那么我们就可以列出要达到的状态的几种情况
...第1种 空串...s第2种 只有一个$s$...sh第3种 有$sh$ 但是还没有完整的$shs$串...shs第4种 第一个$shs$串...shs...s第5种 一个$shs$串加上一个$s$...shs...sh第6种 一个$shs$串加上一个$sh$...shs...shs第7种 两个$shs$串...shs...shs...s第8种 两个$shs$串加上一个$s$...shs...shs...sh第9种 一个$shs$串加上一个$sh$...shs...shs...shs第10种 三个$shs$串,此时已经可以将状态计入合法方案...shs...shs...shs...也是第10种 三个$shs$串,可以将状态计入合法方案
这之后还有很多的状态,但是因为此题中只需要3个$shs$串,所以可以将剩余的状态全部归到...中去,这一步可以说就是完成了状态压缩的步骤
下面我们来考虑dp
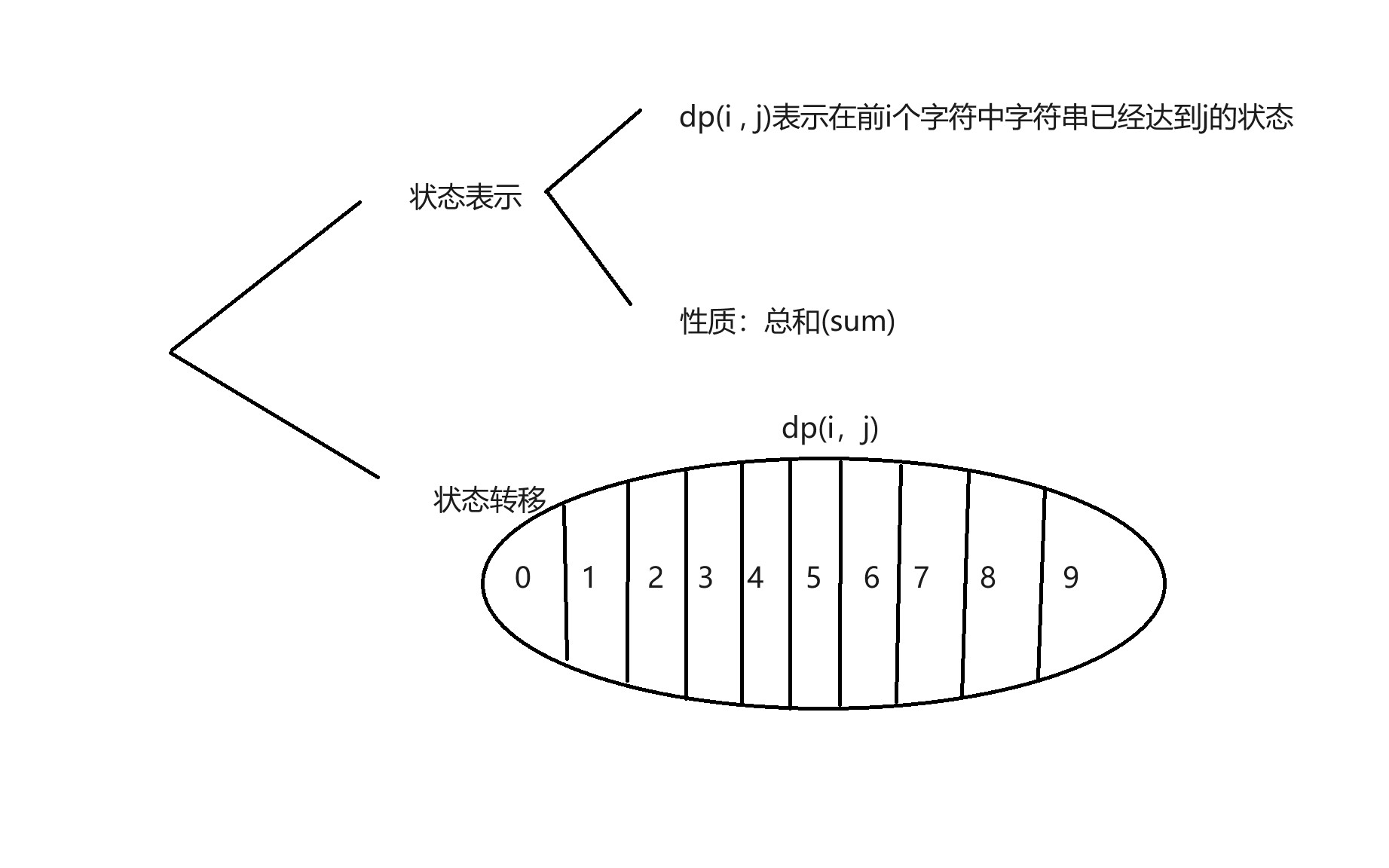
具体转移的自动机如下(注意,之前的状态+1和这里的j对应)
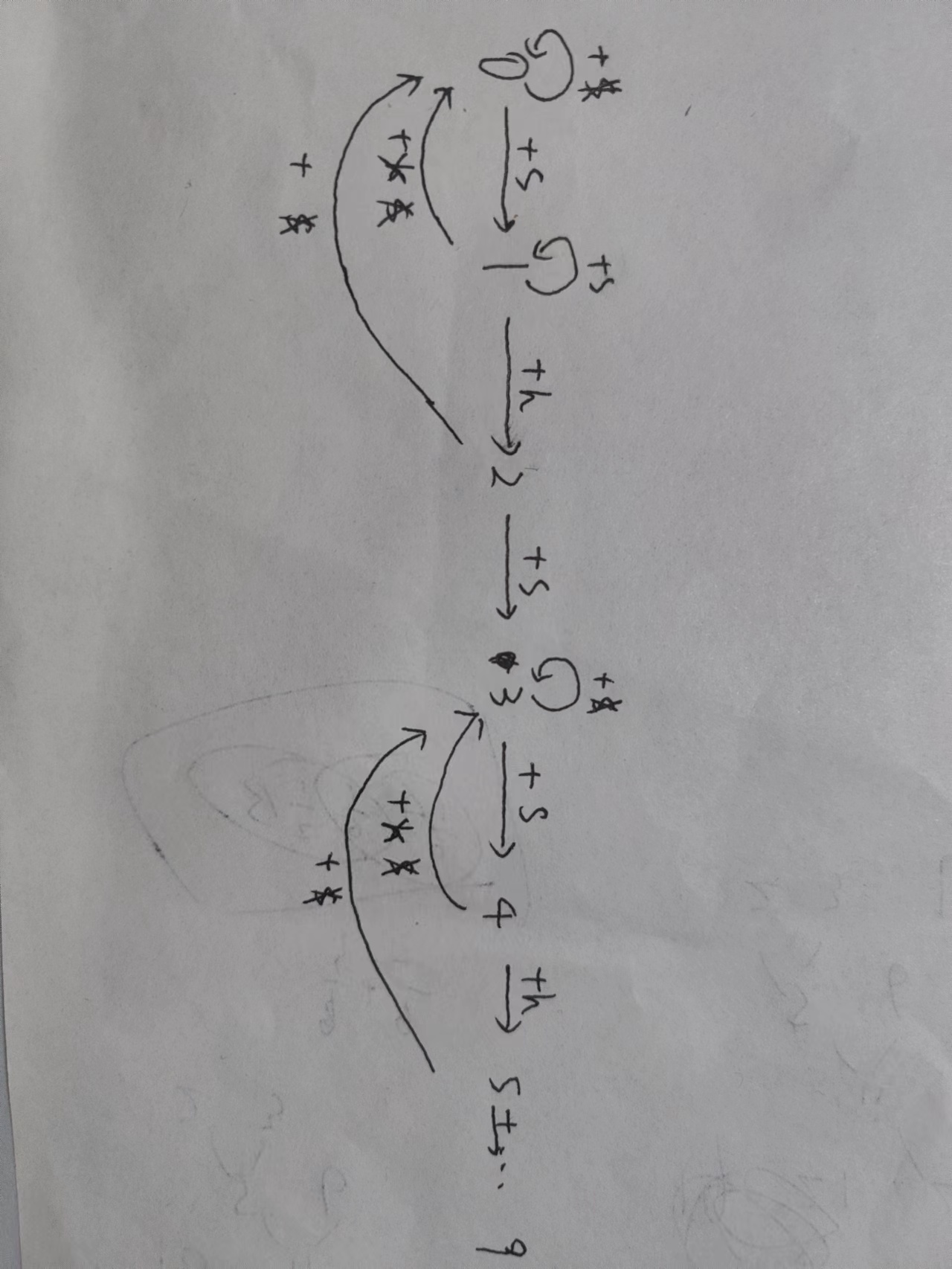
但是很明显我们不可能一个个ifelse去转移方程
其实在写状态转移的时候就会发现有很多状态时相似的
j == 0 || j == 3 || j == 6 是几乎一样的
j == 1 || j == 4 || j == 7 是一样的
j == 2 || j == 5 || j == 8 是一样的
j == 9有两种可能,比较特殊,需要单独讨论
仔细讨论一下转移方程
j == 9时分两种形式,但是无论那种都是合法的,所以后面填什么字母无所谓,因此转移方程
dp[i + 1][j] += dp[i][j] * 26; // 26个字母
j == 1 || j == 4 || j == 7 时
首先是自身+s可以转移
dp[i + 1][j] += dp[i][j];
然后是+h转移到j + 1的状态
dp[i + 1][j + 1] += dp[i][j];
最后是可以+除了s h以外的字母,转移至j - 1的状态
dp[i + 1][j - 1] += dp[i][j] * 24; // 还剩24个字母
剩下的j可以归结成一个
一个是+s转移至下一个状态(完整的shs和单独的s)
dp[i + 1][j + 1] += dp[i][j];
还有一个就是+除了s的其他字母可以转移到0/3/6的状态(2–>0 , 5–>3 , 8–>6)
dp[i + 1][j / 3 * 3] += dp[i][j] * 25; // 还剩25个字母
时间复杂度$O(n)$
然后就是要注意精度 十年OI一场空 不开longlong见祖宗
C++代码
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7 , N = 1000010 , M = 10;
typedef long long LL;
LL dp[N][M] , n;
int main( )
{
cin >> n;
dp[0][0] = 1;
for(int i = 0 ; i < n ; i ++)
for(int j = 0 ; j < 10 ; j ++)
if(j == 9) // 最终状态
{
dp[i + 1][j] = (dp[i + 1][j] + 26 * dp[i][j]) % MOD;
}
else if(j % 3 == 1) // j == 1 || j == 4 || j == 7
{
dp[i + 1][j] = (dp[i + 1][j] + dp[i][j]) % MOD;
dp[i + 1][j + 1] = (dp[i + 1][j + 1] + dp[i][j]) % MOD;
dp[i + 1][j - 1] = (dp[i + 1][j - 1] + 24 * dp[i][j]) % MOD;
}
else
{
dp[i + 1][j + 1] = (dp[i + 1][j + 1] + dp[i][j]) % MOD;
dp[i + 1][j / 3 * 3] = (dp[i + 1][j / 3 * 3] + 25 * dp[i][j]) % MOD;
}
cout << dp[n][9] << '\n';
return 0;
}
如果无法理解为什么把最后的
...shs...shs...shs第10种 三个$shs$串,此时已经可以将状态计入合法方案...shs...shs...shs...也是第10种 三个$shs$串,可以将状态计入合法方案
归结到一块成为一种状态的话,也可以单独拎出来成为第11种状态
...shs...shs...shs...第11种 三个$shs$串,可以将状态计入合法方案
那么
j == 9时,所以后面填什么字母都转移到j == 10,因此转移方程
dp[i + 1][j + 1] += dp[i][j] * 26; // 26个字母
而对于j == 10,后面填什么都可以转移到自身
dp[i + 1][j] += dp[i][j] * 26; // 26个字母
但是这种情况要注意下最后的答案 , j == 9和j == 10 的状态都是答案
C++代码
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7 , N = 1000010 , M = 11;
typedef long long LL;
LL dp[N][M] , n;
int main( )
{
cin >> n;
dp[0][0] = 1;
for(int i = 0 ; i < n ; i ++)
for(int j = 0 ; j < 11 ; j ++)
if(j == 10) // 最终状态
{
dp[i + 1][j] = (dp[i + 1][j] + 26 * dp[i][j]) % MOD;
}
else if(j == 9)
{
dp[i + 1][j + 1] = (dp[i + 1][j + 1] + 26 * dp[i][j]) % MOD;
}
else if(j % 3 == 1) // j == 1 || j == 4 || j == 7
{
dp[i + 1][j] = (dp[i + 1][j] + dp[i][j]) % MOD;
dp[i + 1][j + 1] = (dp[i + 1][j + 1] + dp[i][j]) % MOD;
dp[i + 1][j - 1] = (dp[i + 1][j - 1] + 24 * dp[i][j]) % MOD;
}
else
{
dp[i + 1][j + 1] = (dp[i + 1][j + 1] + dp[i][j]) % MOD;
dp[i + 1][j / 3 * 3] = (dp[i + 1][j / 3 * 3] + 25 * dp[i][j]) % MOD;
}
cout << (dp[n][9] + dp[n][10]) % MOD << '\n';
return 0;
}

