算法一:高斯消元
用来解 n 个方程组成的 n 元 1 次方程组
$\left\{ \begin{aligned} & a_{11}x_1 + a_{12}x_2 + …… + a_{1n}x_n = \;y_1 &(1)\\ & a_{21} x_1 + a_{22} x_2 + …… + a_{2n} x_n = \;y_2 &(2)\\ & …… \\ & a_{n1} x_1 + a_{n2} x_2 + …… + a_{nn} x_n = \;y_n &(n) \end{aligned} \right.$
首先将原方程组变成一个阶梯形方程组
也就是这个样子
$ \left\{ \begin{aligned} a_{11}’x_1 + a_{12}’x_2 + …… + a_{1n}’x_n = \; &\;y_1’ &(1)\\ a_{22}’x_2 + …… + a_{2n}’ x_n = \; &\;y_2’ &(2)\\ ……& \\ a_{nn}’ x_n = \; &\;y_n’ &(n) \end{aligned} \right. $
变化过程:
设当前处理到了第 r 行,第 c 竖列
枚举第 r ~ n 行,对于方程的第 c 竖列我们找到绝对值最大的 $a_{j c}$
然后为了方便操作把第 j 行和第 r 行进行互换
比如
$ \left\{ \begin{aligned} & x_1 + 2x_2 = 5 \;&(1)\\ & 2x_1 + x_2 = 4 \;&(2) \end{aligned} \right. $
挪完1次之后就会变成
$ \left\{ \begin{aligned} & 2x_1 + x_2 = 4 \;&(1)\\ & x_1 + 2x_2 = 5 \;&(2) \end{aligned} \right. $
将第 r 行所有的系数同时除以 $a_{rc}$
这个操作的目的是将 $a_{rc}$ 化成 1
$ \left\{ \begin{aligned} & x_1 + 0.5x_2 = 2 \;&(1)\\ & x_1 + 2x_2 = 5 \;&(2) \end{aligned} \right. $
用下面的几行依次减去第一行的 $a_{ic}$ 倍
这样的话因为 $a_{rc}=1$,所以 $a_{ic}$ 就会清零,同时等式仍然成立
变换后的方程组
$ \left\{ \begin{aligned} x_1 + 0.5x_2 = &\;2 \;&(1)\\ 1.5x_2 = &\;3 \;&(2) \end{aligned} \right. $
然后只需要从后往前算出 $x_i$,再代入前面的方程,就可以解出
$ \left\{ \begin{aligned} & x_1 = 1\\ & x_2 = 2 \end{aligned} \right. $
这是理想状况的结果
还有一种可能就是原方程组无法变成一个完美的阶梯方程组
比如转化完之后的方程组长这样:
$ \left\{ \begin{aligned} x_1 + x_2 + x_3 = &\;3 \;&(1)\\ x_3 = &\;2 \;&(2)\\ 2x_3 = &\;6 \;&(3) \end{aligned} \right. $
出现这种情况的原因是将$a_{21}$归零时$a_{22}$被一起归零
这样的话明显无法确定 $x_1$ 和 $x_2$ 的值,方程有无数组解
还有
$ \left\{ \begin{aligned} x_1 + x_2 = &\;2 \;&(1)\\ 0 = &\;1 \;&(2) \end{aligned} \right. $
由于最后一行所有的系数都被归零,导致出现“零=非零”的矛盾,方程无解
这两种情况需要处理到每一列的时候判断一下最大值是否已经等于 0
int gauss(){
int r,c;
for(c=0,r=0;c<n;c++){
int maxn=r; //找到第c列最大的那一行
for(int i=r+1;i<n;i++)
if(fabs(a[i][c])>fabs(a[maxn][c]))
maxn=i;
if(fabs(a[maxn][c])<zearo) //出现第c列全是0的情况
continue;
for(int i=c;i<=n;i++) //挪到最上面
swap(a[maxn][i],a[r][i]);
for(int i=n;i>=c;i--) //第r行第c列归1
a[r][i]/=a[r][c];
for(int i=r+1;i<n;i++) //其他第c列归0
if(fabs(a[i][c])>zearo)
for(int j=n;j>=c;j--)
a[i][j]-=a[r][j]*a[i][c];
r++;
}
if(r<n){
for(int i=r;i<n;i++)
if(fabs(a[i][n])>zearo) //无解
return 2;
return 1; //无唯一解
}
for(int i=r;i>=0;i--) //从后往前得答案
for(int j=i+1;j<n;j++)
a[i][n]-=a[j][n]*a[i][j];
return 0;
}
本题思路

至于 n 维的球……
我不知道怎么画 n 维的东西
但根据球的定义,n 维的球就是所有与球心距离为半径的点组成的图形
n 维距离公式:
$dist=\sqrt[]{(x_1 - y_1)^2 + (x_2 - y_2)^2 + …… + (x_n - y_n)^2}$
设圆心坐标为 $(x_1,x_2,……,x_n)$,半径为 r
则根据勾股定理可得到方程组
$ \left\{ \begin{aligned} & (b_{11} - x_1)^2 + (b_{12} - x_2)^2 + …… + (b_{1n} - x_n)^2 = r^2 \;&(1)\\ & (b_{21} - x_1)^2 + (b_{22} - x_2)^2 + …… + (b_{2n} - x_n)^2 = r^2 \;&(2)\\ & …… \\ & (b_{n+1\;1} - x_1)^2 + (b_{n+1\;2} - x_2)^2 + …… + (b_{n+1\;n} - x_n)^2 = r^2 \;&(n+1) \end{aligned} \right. $
用完全平方公式展开
$ \left\{ \begin{aligned} & b_{11}^2 + x_1^2 - 2b_{11}x_1 + b_{12}^2 + x_2^2 - 2b_{12}x_2 + …… + b_{1n}^2 + x_n^2 - 2b_{1n}x_n = r^2 \;&(1)\\ & b_{21}^2 + x_1^2 - 2b_{21}x_1 + b_{22}^2 + x_2^2 - 2b_{22}x_2 + …… + b_{2n}^2 + x_n^2 - 2b_{2n}x_n = r^2 \;&(2)\\ & …… \\ & b_{n+1\;1}^2 + x_1^2 - 2b_{n+1\;1}x_1 + b_{n+1\;2}^2 + x_2^2 - 2b_{n+1\;2}x_2 + …… + b_{n+1\;n}^2 + x_n^2 - 2b_{n+1\;n}x_n = r^2 \;&(n+1) \end{aligned} \right. $
然后用方程的第 2 ~ n+1 项分别减去第 1 项
$ \left\{ \begin{aligned} & b_{21}^2 -b_{11}^2 - 2(b_{21} - b_{11})x_1 + …… + b_{2n}^2 -b_{1n}^2 - 2(b_{2n} - b_{1n})x_n = 0 \;&(1)\\ & …… \\ & b_{n+1\;1}^2 -b_{11}^2 - 2(b_{n+1\;1} - b_{11})x_1 + …… + b_{n+1\;n}^2 -b_{1n}^2 - 2(b_{n+1\;n} - b_{1n})x_n = 0 \;&(n) \end{aligned} \right. $
然后整理一下
$ \left\{ \begin{aligned} & 2(b_{21} - b_{11})x_1 + …… + 2(b_{2n} - b_{1n})x_n = b_{21}^2 - b_{11}^2 + …… + b_{2n}^2 -b_{1n}^2\;&(1)\\ & …… \\ & 2(b_{n+1\;1} - b_{11})x_1 + …… + 2(b_{n+1\;n} - b_{1n})x_n = b_{n+1\;1}^2 -b_{11}^2 + …… + b_{n+1\;n}^2 -b_{1n}^2 \;&(n) \end{aligned} \right. $
数据保证有唯一解
所以直接用高斯消元解就行了
完整代码
#include<iostream>
#include<cmath>
using namespace std;
const int N=20;
int n;
double a[N][N],b[N][N];
inline void gauss(){ //高斯消元(不需要处理无解或无唯一解的情况)
for(int i=1;i<=n;i++){
int t=i;
for(int j=i+1;j<=n;j++)
if(fabs(b[j][i])>fabs(b[t][i]))
t=j;
for(int j=i;j<=n+1;j++)
swap(b[t][j],b[i][j]);
for(int j=n+1;j>=i;j--)
b[i][j]/=b[i][i];
for(int j=i+1;j<=n;j++)
for(int k=n+1;k>=i;k--)
b[j][k]-=b[j][i]*b[i][k];
}
for(int i=n;i>1;i--)
for(int j=i-1;j;j--)
b[j][n+1]-=b[i][n+1]*b[j][i];
}
int main(){
scanf("%d",&n);
for(int i=0;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%lf",&a[i][j]);
for(int i=1;i<=n;i++) //得到方程组
for(int j=1;j<=n;j++){
b[i][j]+=2*(a[i][j]-a[0][j]);
b[i][n+1]+=a[i][j]*a[i][j]-a[0][j]*a[0][j];
}
gauss();
for(int i=1;i<=n;i++)
printf("%.3lf ",b[i][n+1]);
return 0;
}
算法二:模拟退火
理论上来讲这是个随机算法……
不过是科学的随机
就是设定一个温度和一个位置,然后在当前位置附近以温度为范围随机跳
如果跳到的位置比当前位置更优就会保留新的位置
如果跳到的位置没有当前位置优也要有一定的概率保留,这个概率取决于劣了多少
这样做的目的是为了避免取到局部最优解
跳的过程中温度会以一定的比例不断降低
这样跳的过程中就有可能获得最优解
注意:只是有可能获得,还有一定的可能获得的不是最优解
所以一般情况下会重复若干次这个过程,然后在所有的结果里面取得最优的一个
inline double rand(double l,double r){
return (double)rand()/RAND_MAX*(r-l)+l;
}
inline void simulate_anneal(){
double cur=rand(0,10000); //这是只有一个随机数的情况,随机范围是根据题目调整的常数
for(double t=1e4;t>1e-4;t*=0.9){ //初始值、最终值、递减比例都是要根据题目调整的常数
double np=rand(cur.first-t,cur.first+t);
double dt=calc(np)-calc(cur); //这里的calc是题目决定的计算方法
if(exp(-dt/t)>rand(0,1))
cur=np;
}
}
本题思路
还是根据球的定义,球心到球面所有点的距离相等,也就是说距离的波动为零
这道题要考虑当前取到的点到圆面上点距离的波动情况
所以计算方法就是方差
注意:模拟退火算法适合随机的数不那么多的题,此题不建议用这个方法,常数贼难调
完整代码
#include<iostream>
#include<cmath>
#include<ctime>
using namespace std;
typedef pair<double,double> PDD;
const int N=20;
int n;
double a[N][N];
double cur[N],np[N];
double d[N];
double ans[N],minans=1e18;
PDD q[N];
inline double rand(double l,double r){
l=max(l,-2e4); //为了不计算无价值的点手动更改范围
r=max(r,-2e4);
l=min(l,2e4);
r=min(r,2e4);
return (double)rand()/RAND_MAX*(r-l)+l;
}
inline double dist(double a[],double b[]){ //为了卡精度不进行开根
double sum=0;
for(int i=1;i<=n;i++){
double d=a[i]-b[i];
sum+=d*d;
}
return sum;
}
inline double calc(double p[]){
double avg=0,res=0;
for(int i=1;i<=n+1;i++){
d[i]=dist(p,a[i]);
avg+=d[i];
}
avg/=n+1;
for(int i=1;i<=n+1;i++){
double dif=avg-d[i];
res+=dif*dif;
}
//为了卡精度res不除以n+1,不是严格意义上的方差
if(res<minans){ //更新答案
for(int i=1;i<=n;i++)
ans[i]=p[i];
minans=res;
}
return res;
}
inline void simulate_anneal(){ //模拟退火函数
for(int i=1;i<=n;i++) //生成n维的随机点
cur[i]=rand(-20000,20000);
for(double t=20000;t>1e-6;t*=0.9999){ //温度
for(int i=1;i<=n;i++)
np[i]=rand(cur[i]-t,cur[i]+t); //随机跳
double dt=calc(np)-calc(cur);
if(exp(-dt/t)>rand(0,1))
for(int i=1;i<=n;i++) //保留结果
cur[i]=np[i];
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n+1;i++)
for(int j=1;j<=n;j++)
scanf("%lf",&a[i][j]);
while((double)clock()/CLOCKS_PER_SEC<0.8) //卡时间,运行直到时间到达0.8s
simulate_anneal();
for(int i=1;i<=n;i++)
printf("%.3lf ",ans[i]);
return 0;
}
算法三:爬山法
爬山法可以算是模拟退火的一个变种,适用于单峰函数
区别在于每次根据当前点的状态确定一个大致方向,然后沿该方向移动一定距离
这个移动距离根据当前答案到底有多劣以及现在的温度确定的
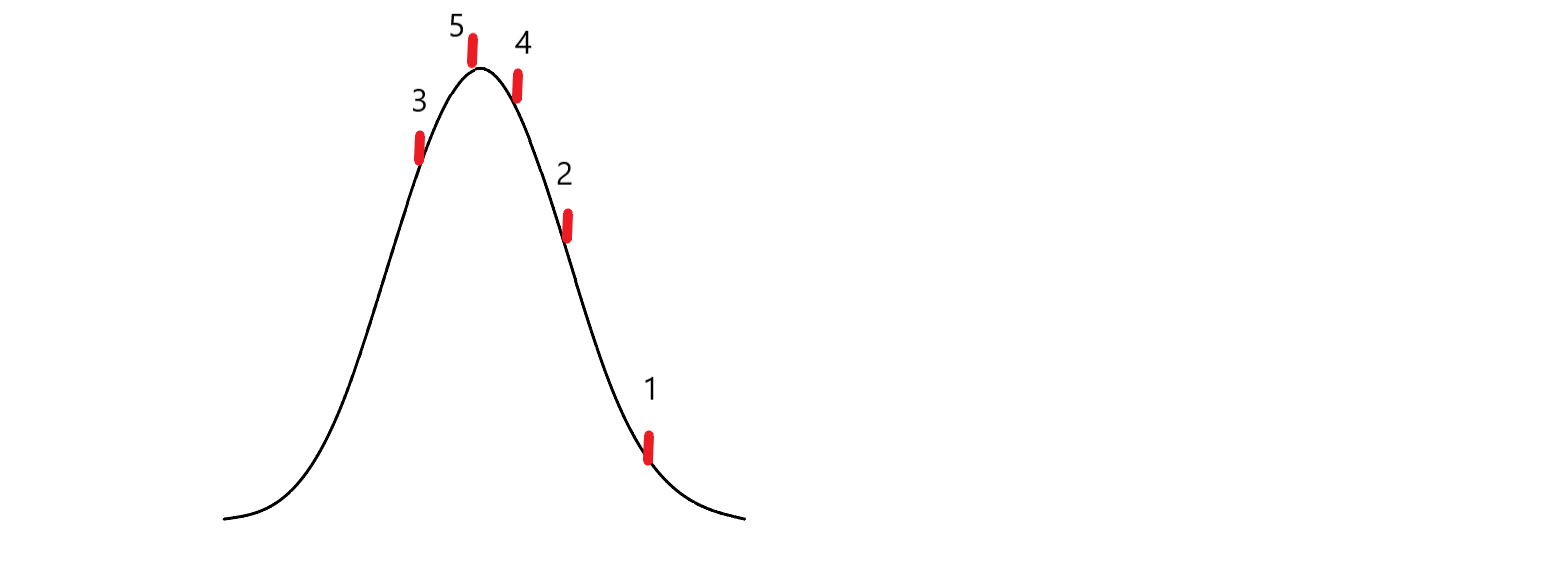
这样温度最后降到一定程度获得的答案就会非常接近正解
距离是二次函数,所以只考虑n维的其中1维时此题明显是一个单峰函数
我们的目的是要使点到圆面上所有点的距离相等
如果圆面上某个点到当前点的距离大于平均距离,就需要靠近这个点,反之则需要远离这个点
一种符合条件的计算方法:
$delta_j = (\sum_{i = 1}^{n+1}\frac{(dist_i - \overline{dist})(a_{ij} - ans_j)}{\overline{dist}})t$
这里的$delta_j$代表第j维要移动的距离
还有其他的计算方法也适用于这个题,不过精度上有一定不同,大家可以自行尝试
完整代码
#include<iostream>
#include<cmath>
using namespace std;
const int N=20;
int n;
double a[N][N];
double ans[N],dist[N],delta[N];
inline void calc(){
double avg=0; //平均距离
for(int i=1;i<=n+1;i++){
dist[i]=delta[i]=0;
for(int j=1;j<=n;j++)
dist[i]+=(a[i][j]-ans[j])*(a[i][j]-ans[j]);
dist[i]=sqrt(dist[i]);
avg+=dist[i]/(n+1);
}
for(int i=1;i<=n+1;i++)
for(int j=1;j<=n;j++)
delta[j]+=(dist[i]-avg)*(a[i][j]-ans[j])/avg; //计算移动距离
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n+1;i++)
for(int j=1;j<=n;j++){
scanf("%lf",&a[i][j]);
ans[j]+=a[i][j]/(n+1);
}
for(double t=1e4;t>1e-6;t*=0.99995){ //温度
calc();
for(int i=1;i<=n;i++)
ans[i]+=delta[i]*t;
}
for(int i=1;i<=n;i++)
if(fabs(ans[i])<1e-4) //避免出现“负零”
printf("0.000 ");
else
printf("%.3lf ",ans[i]);
return 0;
}

