思路

由于操作对下标顺序没有限制，可将所有塔的高度升序排序后考虑。

性质：

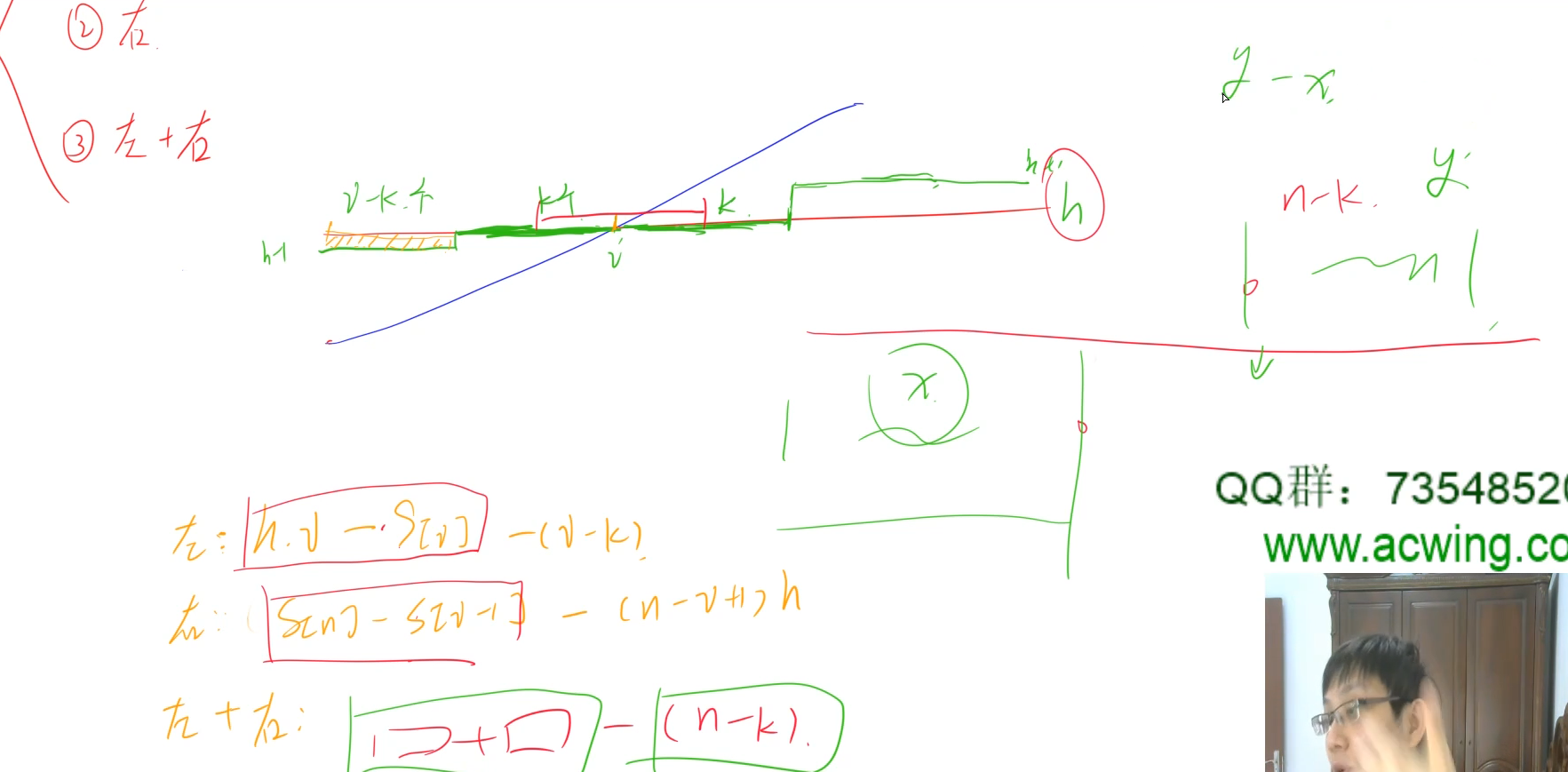
1. 最优解高度一定不能小于零或大于最高塔高度。以小于零为例，此时只能从最高的塔开始削，一定不如把解的高度定为等于零。同理，大于最高塔高度一定不如等于它。
2. 最优解高度一定等于某个塔的高度。假设它介于两个塔的高度之间，若总是操作最低的塔，则不如把解的高度下降为当前高度下方塔的高度。若总是操作最高的塔，则不如把解的高度升高为当前高度上方塔的高度。若既操作最低的塔，又操作最高的塔，假设左边使得 $x$ 座塔到达目标高度，右边使得 $y$ 座塔到达目标高度，若 $x > y$，则将高度降为下界更优，否则升为上界更优。
3. 假设一边有 $x$ 座塔到达目标高度，则剩余塔一定被操作到目标高度减一，因为所支持的两种规则必然让某一边只能一层层操作。

枚举解的高度，对于当前高度，只有三类方案，要么只操作最低的塔，要么只操作最高的塔，要么既操作最低的塔，又操作最高的塔。无论如何，可 $O(1)$ 得到操作次数。

CPP

高度很小，从小到大枚举整个高度范围，省去排序，$O(a)$。

#include <iostream>

using namespace std;

constexpr int N = 10010;

int n, k;
int cnt[N]; // cnt[i] 高度为 i 的塔的数量
int s[N];   // s[i] 高度小于等于 i 的塔的高度之和

int main() {
  cin >> n >> k;

  int mx_cnt = -1;
  for (int i = 0; i < n; i++) {
    int h;
    cin >> h;
    cnt[h]++;
    mx_cnt = max(mx_cnt, cnt[h]);
  }

  if (mx_cnt >= k) {
    cout << 0 << endl;
    return 0;
  }

  for (int i = 1; i <= N; i++)
    s[i] = s[i - 1] + i * cnt[i];

  int res = 2e9;
  // sc 高度小于 i 的塔的数量，把高度为 i 的塔划到右边
  for (int i = 1, sc = 0; i <= N; i++) {
    // 左边 i 以下，原始塔高以上面积，不包含高度 i
    int left = sc * i - s[i - 1];
    // 右边 i 以上，原始塔高以下面积，不包含高度 i（因为它们已就绪）
    int right = s[N] - s[i] - (n - sc - cnt[i]) * i;

    // cnt[i] 座已就绪，只需再操作 k - cnt[i] 座
    if (sc >= k - cnt[i]) res = min(res, left - (sc - (k - cnt[i])));
    // 最右 n - sc - k 座高度为 i - 1
    if (n - sc >= k) res = min(res, right - (n - sc - k));

    // k 座高度为 i，n - k 座高度为 i - 1
    res = min(res, left + right - (n - k));
    sc += cnt[i];
  }
  cout << res << endl;

  return 0;
}

JAVA

若高度很大，先排序，$O(nlogn)$。

import java.io.*;
import java.util.*;

public class Main {

  static int gi(StreamTokenizer t) throws Exception {
    t.nextToken();
    return (int) t.nval;
  }

  public static void main(String[] args) throws Exception {
    var r = new BufferedReader(new InputStreamReader(System.in));
    var t = new StreamTokenizer(r);
    final int N = 200010;
    int n, k;
    int a[] = new int[N], s[] = new int[N];

    n = gi(t);
    k = gi(t);

    for (int i = 1; i <= n; i++) a[i] = gi(t);

    Arrays.sort(a, 1, n + 1);

    for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];

    int res = (int)2e9;
    for (int i = 1; i <= n; i++) {
      int j = i;
      while (j <= n && a[i] == a[j]) j++;
      int cAi = j - i;
      if (cAi >= k) {
        res = 0;
        break;
      }

      int left = (i - 1) * a[i] - s[i - 1];
      int right = s[n] - s[j - 1] - (n - j + 1) * a[i];
      if (i - 1 >= k - cAi) res = Math.min(res, left - (i - 1 - (k - cAi)));
      if (n - (i - 1) >= k) res = Math.min(res, right - (n - (i - 1) - k));

      res = Math.min(res, left + right - (n - k));

      i = j - 1;
    }

    System.out.println(res);

    r.close();
  }
}