题目描述

难度分:$1700$

输入$T(\leq 10^4)$表示$T$组数据。所有数据的$n \times m$之和$\leq 10^6$。

每组数据输入$n$，$m(1 \leq n \times m \leq 10^6)$和长为$n \times m$的$01$字符串$s$。

有$n \times m$个人参加会议，会议厅的座位有$n$行$m$列。

从第一个人开始，依次入场。规则如下：

有人入场时，已入场的人同时向右移动一位，最右的人移动到下一行的最左边。（见样例）

第$i$个人标记为$s[i]$。

输出$n \times m$个数，其中第$i$个数表示：第$i$个人入场后，至少有一个$1$的行数+至少有一个$1$的列数？

输入样例

3
2 2
1100
4 2
11001101
2 4
11001101

输出样例

2 3 4 3
2 3 4 3 5 4 6 5
2 3 3 3 4 4 4 5

样例的第一个数据如下

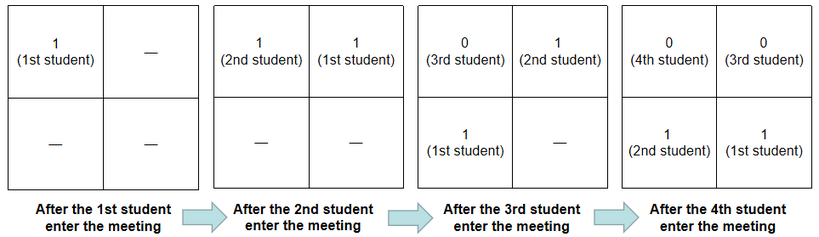
算法

滑动窗口+动态规划

统计列

$s[i]$，$s[i-m]$，$s[i-2m]$，……是属于同一列的，因此只要出现$s[i]=1$，说明这一列就可以被计入答案了，用一个数组$col_{1 \times m}$来标记每一列是否出现过$1$即可。

统计行

状态定义

$dp[i]$表示遍历到$s[i]$时有多少行是有$1$的。

状态转移

用一个长度为$m$的窗口$window$来记录第一行$[i,i-m)$内$1$的数量，这样状态转移方程就为

$dp[i]=dp[i-m]+(window>0)$

复杂度分析

时间复杂度

对于每个$case$，都只遍历了一遍字符串$s$就统计出了所有答案，因此时间复杂度为$O(Tnm)$。

空间复杂度

额外空间的瓶颈在于$DP$数组，其规模与$s$相同，因此额外空间复杂度为$O(nm)$（可以滚动数组优化到$O(m)$）。

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;
int T, n, m;

int main() {
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        string s;
        cin >> s;
        vector<int> col(m), dp(n*m);
        int ccnt = 0, window = 0;
        for(int i = 0; i < n*m; i++) {
            if(s[i] == '1' && !col[i%m]) {
                col[i%m] = true;
                ccnt++;
            }
            window += s[i] == '1'? 1: 0;
            if(i >= m) {
                window -= s[i - m] == '1'? 1: 0;
            }
            if(i >= m) {
                dp[i] = dp[i - m] + (window > 0? 1: 0);
            }else {
                dp[i] = window > 0? 1: 0;
            }
            printf("%d ", ccnt + dp[i]);
        }
        puts("");
    }
    return 0;
}