熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。

小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列。

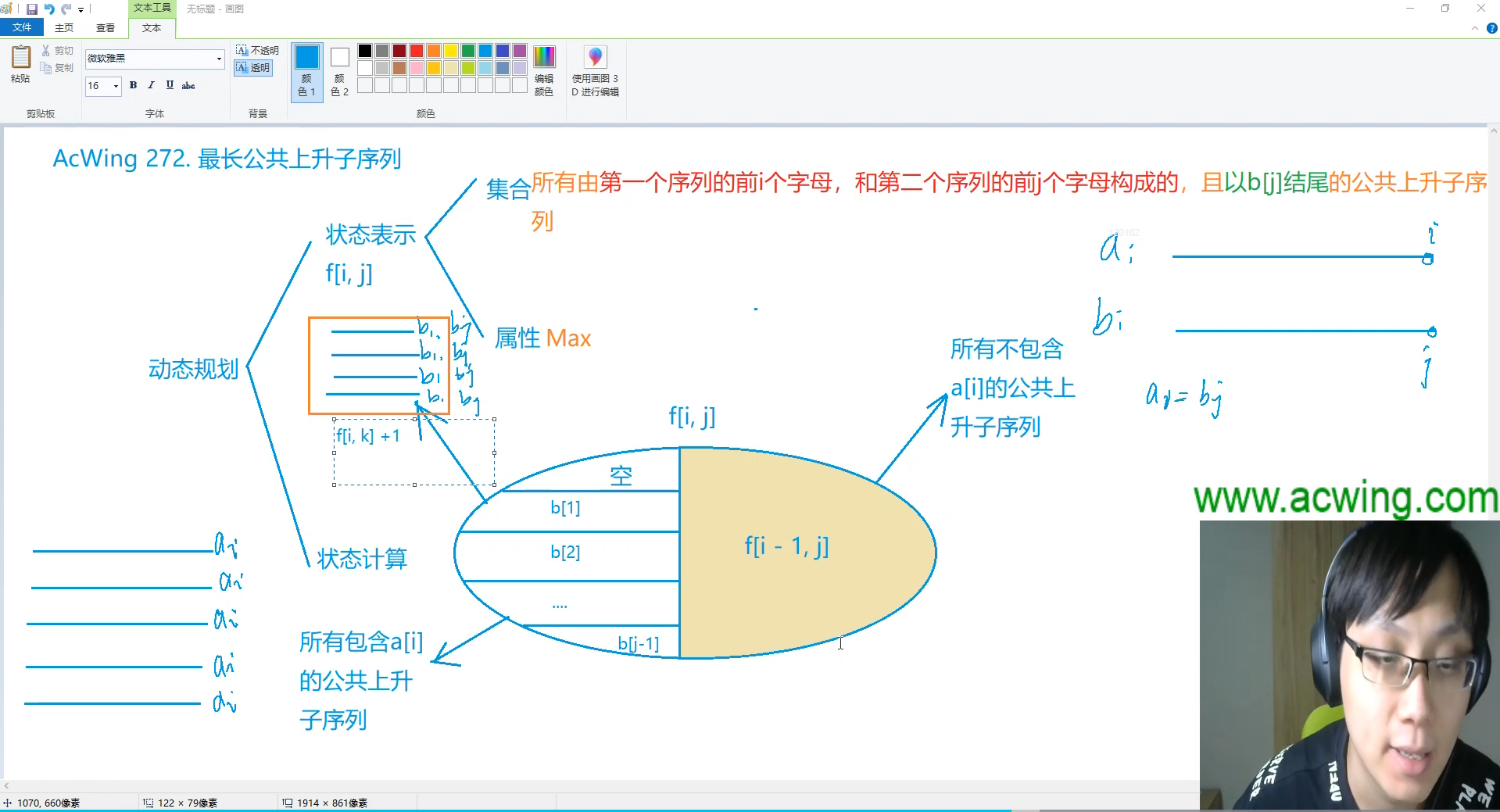
小沐沐说，对于两个数列 $A$和 $B$，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。

奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。

不过，只要告诉奶牛它的长度就可以了。

数列 $A$和 $B$ 的长度均不超过 $3000$。

输入格式

第一行包含一个整数 $N$，表示数列 $A，B$的长度。

第二行包含 $N$个整数，表示数列 $A$。

第三行包含 $N$个整数，表示数列 B$$。

输出格式

输出一个整数，表示最长公共上升子序列的长度。

数据范围

$1≤N≤3000$,序列中的数字均不超过 $23^1−1$。

输入样例：

4
2 2 1 3
2 1 2 3

输出样例：

2

#include <iostream>

using namespace std;

const int N = 3010;

int n, ans, f[N][N], a[N], b[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++) cin >> a[i];
    for (int i = 1; i <= n; i ++) cin >> b[i];

    for (int i = 1; i <= n; i ++)
    {
        int maxv = 1;
        for (int j = 1; j <= n; j ++)
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(maxv, f[i][j]);
            if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }

    for (int i = 1; i <= n; i ++) ans = max(ans, f[n][i]);

    cout << ans;

    return 0;
}