有 $N$ 种物品和一个容量是 $V$的背包。

第 $i$种物品最多有 $s_i$ 件，每件体积是 $v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，$N$，$V(0<N≤1000, 0<V≤20000)$，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$行，每行三个整数 $v_i,w_i,s_i$，用空格隔开，分别表示第 $i$种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

$0<N≤1000$

$0<V≤20000$
$0<v_i,w_i,s_i≤20000$

提示

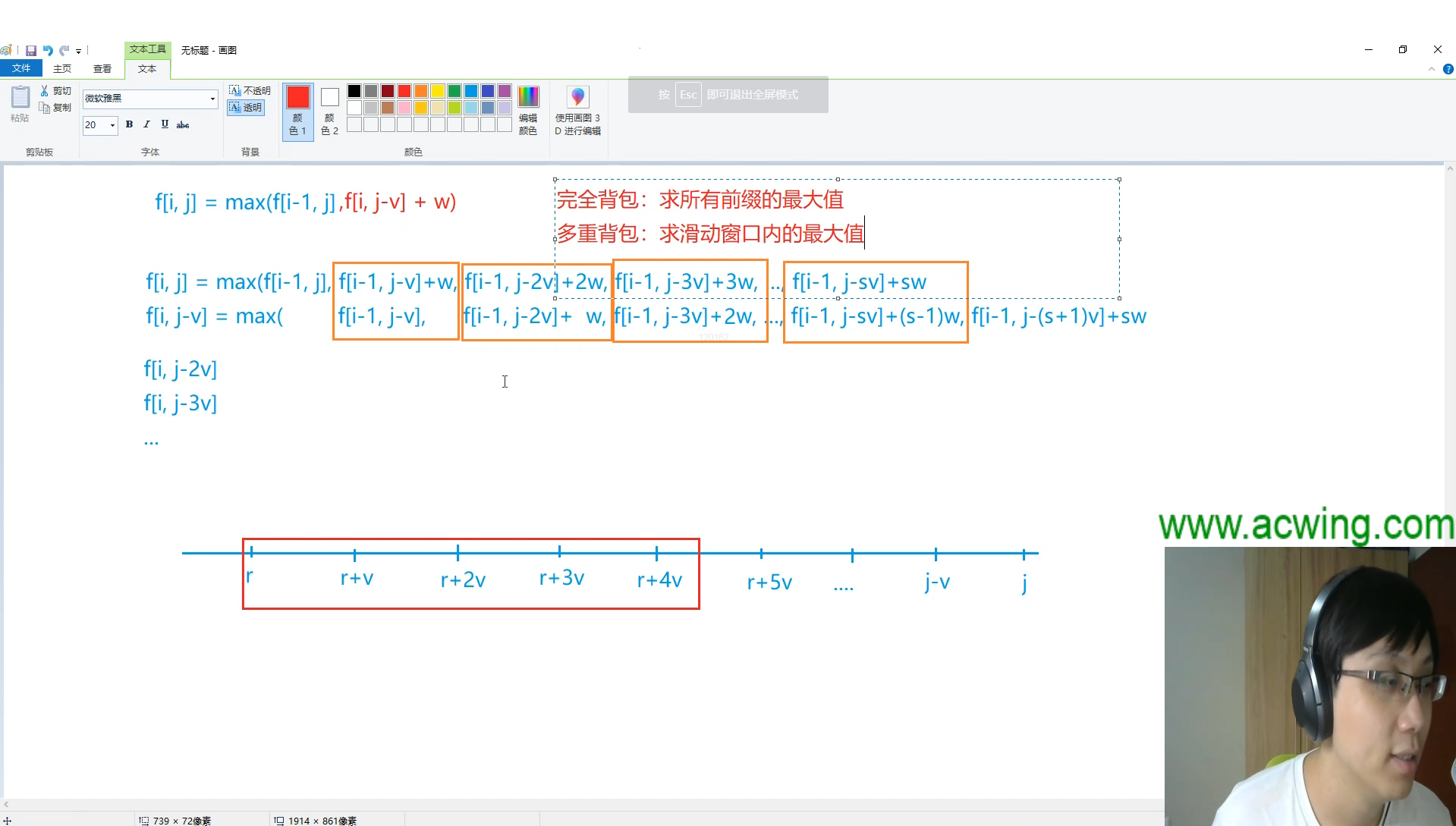
本题考查多重背包的单调队列优化方法。

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

#include <cstring>
#include <iostream>

using namespace std;

const int N = 20010;

int n, m;
int f[N], g[N], q[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);
        for (int j = 0; j < v; j ++)
        {
            int hh = 0, tt = -1;
            for (int k = j; k <= m; k += v)
            {
                if (hh <= tt && q[hh] < k - s * v) hh ++; // 删除超出长度元素
                if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w); // 更新答案
                while (hh <= tt && g[q[tt]] <= g[k] - (k - q[tt]) / v * w) tt -- ; // 维护单调性
                q[++ tt] = k;
            }
        }
    }
    cout << f[m];

    return 0;
}