宣传一下算法提高课整理 <—

CSDN个人主页：更好的阅读体验 <—

本题链接（AcWing） 点这里

题目描述

有 $N$ 个物品和一个容量是 $V$ 的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

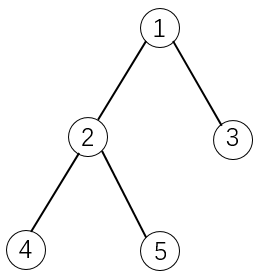
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 $i$，体积是 $v_i$，价值是 $w_i$，依赖的父节点编号是 $p_i$。物品的下标范围是 $1 … N$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 $N，V$，用空格隔开，分别表示物品个数和背包容量。

接下来有 $N$ 行数据，每行数据表示一个物品。
第 $i$ 行有三个整数 $v_i, w_i, p_i$，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 $p_i = -1$，表示根节点。 数据保证所有物品构成一棵树。

输出格式

输出一个整数，表示最大价值。

数据范围

$1 \le N, V \le 100$
$1 \le v_i, w_i \le 100$

父节点编号范围：

• 内部结点：$1 \le p_i \le N$;
• 根节点 $p_i = -1$;

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例

11

思路

本题为DP问题，可以使用 闫氏DP分析法 解题。

主要思想：枚举每个状态分给各个子节点的体积

DP：

• 状态表示 $f(i,j)$：
  • 集合：考虑第 $i$ 个物品为根节点的子树，且选上 $i$，选法的总体积不超过 $j$ 的所有方案。
  • 属性：$\max$
• 状态计算：f[s[i]][j]表示 i 所有子节点共用体积 j 的选法的最大值
  • 不选第 $i$ 个物品：0
  • 选第 $i$ 个物品且体积不超过 $0$：max{f[s[i]][0] + w[i]}
  • 选第 $i$ 个物品且体积不超过 $1$：max{f[s[i]][1] + w[i]}
  • 选第 $i$ 个物品且体积不超过 $2$：max{f[s[i]][2] + w[i]}
  • 选第 $i$ 个物品且体积不超过 $j - v_i$：max{f[s[i]][j - v[i]] + w[i]}

时间复杂度：$O(n \times V^2)$

AC Code:

$C++$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110;

int n, m;
int h[N], e[N], ne[N], idx;
int v[N], w[N];
int f[N][N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int s = e[i];
        dfs(s);

        for (int j = m - v[u]; j >= 0; j -- )
            for (int k = 0; k <= j; k ++ )
                f[u][j] = max(f[u][j], f[u][j - k] + f[s][k]);
    }

    for (int i = m; i >= v[u]; i -- )
        f[u][i] = f[u][i - v[u]] + w[u];
    for (int i = 0; i < v[u]; i ++ )
        f[u][i] = 0;
}

int main()
{
    cin >> n >> m;

    memset(h, -1, sizeof h);
    int root;
    for (int i = 1; i <= n; i ++ )
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else add(p, i);
    }

    dfs(root);

    cout << f[root][m] << endl;

    return 0;
}

最后，如果觉得对您有帮助的话，点个赞再走吧！