C++

$\color{gold}{— > 蓝桥杯辅导课题解}$

思路：

dp — 区间dp

$在回文串中加上一个数与减去对应的另外一个数是等价的$

$例：3男和1女匹配，需要加上2女和减去2男才能完成匹配的数量是一样的$

                                                闫氏dp分析法

                集合：所有s[l ~ r]之间回文子序列的集合                                    
    状态表示
                属性：长度的最大值max
dp

    状态计算    是否选择 l, r

                选l, r：f[l + 1][r - 1] + 2
                选l, 不选r：f[l][r - 1]
                不选l, 选r：f[l + 1][r]
                不选l, 不选r：f[l + 1][r - 1]

                取max

$状态计算：$

$选l, r$

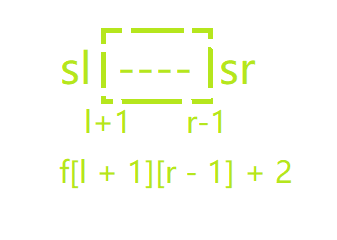
$选l, 不选r$

$不选l, 选r$

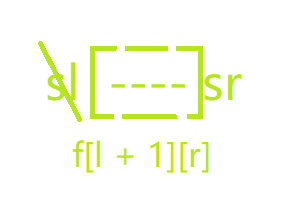
$不选l, 不选r$

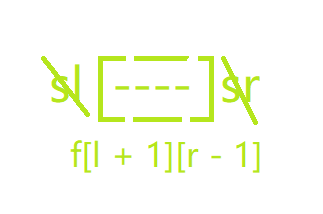
$code$

$time\ complexity：O(n^2)$

#include <bits/stdc++.h>
using namespace std;

const int N = 1010;

char s[N];
int f[N][N];

int main() {
    cin >> s;
    int n = strlen(s);

    for (int len = 1; len <= n; len ++) // 长度
        for (int l = 0; l + len - 1 < n; l ++) { // 左端点
            int r = len + l - 1; // 右端点
            if (len == 1) f[l][r] = 1;
            else {
                if (s[l] == s[r]) f[l][r] = f[l + 1][r - 1] + 2;
                if (f[l][r - 1] > f[l][r]) f[l][r] = f[l][r - 1];
                if (f[l + 1][r] > f[l][r]) f[l][r] = f[l + 1][r];
            }
        }

    cout << n - f[0][n - 1]; // 由于f[l][r]求的是最长的已经匹配好的回文子序列，所以需要n-f[0][n - 1]

    return 0;
}