换根DP

此题与 STA-Station - POI2008 思路有些许类似

与以往的换根DP分类方式相似，从节点u出发的路径分为两类：

1. 从u往其子节点走的所有路径
2. 从u到其父节点往上走的路径

树中任何节点到节点u的距离之和，等价于这两类路径的长度之和

因此，我们就可以维护两个数组：d[u]和up[u]，分别表示从节点u往下的距离之和以及从节点u往上走的距离之和

对于维护d[]：

假设存在一条边：x -> y，那么d[x] = d[y] + cnt[y]，其中cnt[y]表示以y为根的子树的节点数量

原因：d[x]与d[y]的区别只有x -> y的边，而累加的次数就是以y为根的子树到节点x的边数，即以y为根的子树的节点数量

因此考虑自底向上维护d[]

而cnt[]比较好维护：cnt[x] += cnt[y]，以x为根的子树的节点数量，等价于其所有子树的节点数量加上u本身

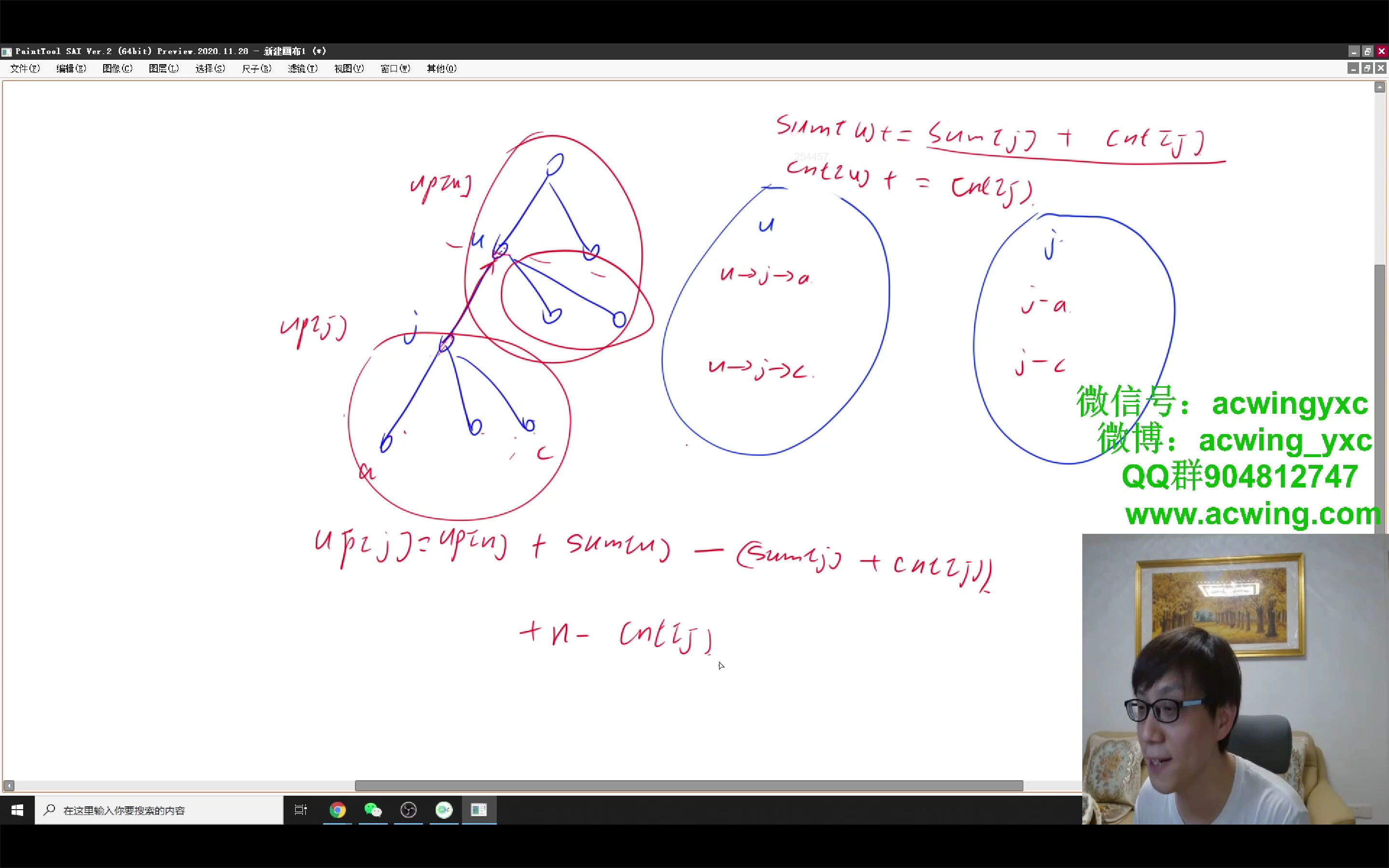
对于维护up[]：

up[j] = up[u] + d[u] - (d[j] + cnt[j]) + n - cnt[j];

父节点往上走的距离之和 + 父节点往下走且不经过j的所有路径的距离之和 + 往上走的节点总数

C++ Code: vector

class Solution {
public:
    vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
        vector<int> d(n), up(n), cnt(n);
        // 建图
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b), g[b].push_back(a);
        }

        function<void(int, int)> dfs_d = [&](int u, int fa) {
            d[u] = 0;
            cnt[u] = 1;
            for (int x : g[u]) {
                if (x == fa) continue;
                dfs_d(x, u);  // 自底向上维护
                cnt[u] += cnt[x];
                d[u] += d[x] + cnt[x];
            }
        };
        dfs_d(0, -1);

        function<void(int, int)> dfs_u = [&](int u, int fa) {
            for (int x : g[u]) {
                if (x == fa) continue;
                up[x] = up[u] + d[u] 
                - (d[x] + cnt[x]) // 减去 x 的分支的总和
                + n - cnt[x]; // 往上的节点总数 
                dfs_u(x, u); // 自项向下维护
            }
        };
        dfs_u(0, -1);

        vector<int> res;
        for (int i = 0; i < n; i ++ )
            res.push_back(d[i] + up[i]);
        return res;
    }
};

C++ Code: 数组

const int N = 30010, M = N << 1;

int h[N], e[M], ne[M], idx;
int sum[N], cnt[N], up[N];

/*

1. sum[u] : 表示从节点 u 向下走的距离之和
2. cnt[u] : 表示以 u 为根的子树的节点数量
3. up[u] : 表示从节点 u 往上走的所有距离之和

*/

class Solution {
public:

    int n;

    void add(int a, int b) {
        e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
    }

    void dfs_d(int u, int fa) {
        sum[u] = 0;
        cnt[u] = 1;
        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (j == fa) continue;
            dfs_d(j, u);
            sum[u] += sum[j] + cnt[j]; 
            cnt[u] += cnt[j];
        }
    }

    void dfs_u(int u, int fa) {
        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (j == fa) continue;
            up[j] = up[u] + sum[u] - (sum[j] + cnt[j]) + n - cnt[j];
            dfs_u(j, u);
        }
    }

    vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) {
        memset(h, -1, sizeof h);
        idx = 0;
        n = N;
        for (auto& e: edges) {
            int x = e[0], y = e[1];
            add(x, y), add(y, x); // 无向边
        }

        dfs_d(0, -1);
        dfs_u(0, -1);

        vector<int> res;
        for (int i = 0; i < n; i ++ )
            res.push_back(sum[i] + up[i]);

        return res;
    }
};

Python3 Code

class Solution:
    def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
        d = [0] * n
        up = [0] * n
        cnt = [0] * n
        # 建图
        g = [[] for _ in range(n + 1)]
        for x, y in edges:
            g[x].append(y)
            g[y].append(x)

        def dfs_d(u: int, fa: int) -> None:
            cnt[u] = 1
            d[u] = 0
            for x in g[u]:
                if (x != fa):
                    dfs_d(x, u)
                    cnt[u] += cnt[x]
                    d[u] += d[x] + cnt[x]
        dfs_d(0, -1)

        def dfs_u(u: int, fa: int) -> None:
            for x in g[u]:
                if (x != fa):
                    up[x] = up[u] + d[u] - (d[x] + cnt[x]) + n - cnt[x]
                    dfs_u(x, u)
        dfs_u(0, -1)

        res = []
        for i in range(n):
            res.append(d[i] + up[i])
        return res