$$\color{Red}{战略游戏-简单的状态机融合}$$

这里附带打个广告——————我做的所有的题解

包括基础提高以及一些零散刷的各种各样的题

题目介绍

鲍勃喜欢玩电脑游戏，特别是战略游戏，但有时他找不到解决问题的方法，这让他很伤心。

现在他有以下问题。

他必须保护一座中世纪城市，这条城市的道路构成了一棵树。

每个节点上的士兵可以观察到所有和这个点相连的边。

他必须在节点上放置最少数量的士兵，以便他们可以观察到所有的边。

你能帮助他吗？

例如，下面的树：

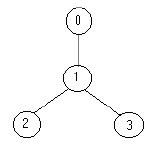
只需要放置 1 名士兵（在节点 1 处），就可观察到所有的边。
输入格式

输入包含多组测试数据，每组测试数据用以描述一棵树。

对于每组测试数据，第一行包含整数 N，表示树的节点数目。

接下来 N 行，每行按如下方法描述一个节点。

节点编号：(子节点数目) 子节点 子节点。

节点编号从 0 到 N−1，每个节点的子节点数量均不超过 10，每个边在输入数据中只出现一次。

输出格式
对于每组测试数据，输出一个占据一行的结果，表示最少需要的士兵数。

数据范围

0 < N ≤ 1500

一个测试点所有 N 相加之和不超过 300650。

输入样例：

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

输出样例：

1
2

树形DP：dfs结合dp

我的没有上司的舞会题解 类似的一道题目，也是状态机相关的树形dp

1.算法细节

• 不难看出，此题和树的重心 类似，只是存值使用了两个维度的状态表达式，但是为什么树的重心我们采用了st的bool数组，代表一个点是否可以遍历到，本题却不用了呢？

非常简单，树的重心是无向图，我们在求一颗确定根节点的树的结点数量，利用了这些边去遍历结点，我们使用st的bool数组是为了防止遍历过程中走到根节点之上，陷入死循环。
本题是有向图，故不会出现遍历到根节点的可能。

• 如何设计状态表达式和状态方程？为什么计算各不相同？

极小点覆盖是指在一个图中，选出最少的顶点，使得每条边至少有一个端点被选中。

本题的节点关系以一颗树的图来保存，一个位置i是否放士兵用状态0和1表示。

f[i][j（0 -> 不放 / 1 -> 放）]:代表着i节点位置放士兵或不放的集合，取最小值。状态方程计算各不相同。

这里是状态机的思想，但是节点位置之间的关系使用的是树来存储和线性不同

f[root][0] = f[son 1][1] + f[son 2][1] + '''' + f[son n][1]
f[root][1] = min(min(f[son 1][0], f[son 1][1]) + min(f[son 2][0], f[son 2][1]) + '''' + min(f[son n][0], f[son n][1]))

一个地方放士兵的最小值应该是他的一个个的邻接点位置放或不放的方案的最小值求和转移而来。
而一个位置不放，应该是一个个邻接点位置必须放士兵的求和转移而来。

2.具体代码

java

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int N = 1510, idx, n;
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] h = new int[N];
    static boolean[] st = new boolean[N];
    static int[][] f = new int[N][N];

    static void add(int x, int y) {
        e[idx] = y;
        ne[idx] = h[x];
        h[x] = idx++;
    }

    static void dfs(int x) {
        f[x][1] = 1;
        f[x][0] = 0;
        for (int i = h[x]; i != -1; i=ne[i]) {
            int son = e[i];
            dfs(son);
            f[x][1] += Math.min(f[son][0], f[son][1]);
            f[x][0] += f[son][1];
        }
    }

    static Scanner sc = new Scanner(System.in);

    public static void main(String[] args) {
        while (sc.hasNext()) {
            n = sc.nextInt();
            idx = 0;
            Arrays.fill(h, -1);
            Arrays.fill(st, false);
            for (int i = 0; i < n; i++) {
                String s = sc.next();
                int father = Integer.parseInt(s.substring(0, s.indexOf(":")));
                int num = Integer.parseInt(s.substring(s.indexOf("(") + 1, s.indexOf(")")));
                for (int j = 0; j < num; j++) {
                    int son = sc.nextInt();
                    add(father, son);
                    st[son] = true;
                }
            }
            int root = 0;
            while(st[root]) root++;
            dfs(root);
            System.out.println(Math.min(f[root][1], f[root][0]));
        }
    }
}