楼兰图腾

只解释每个函数或者变量的含义

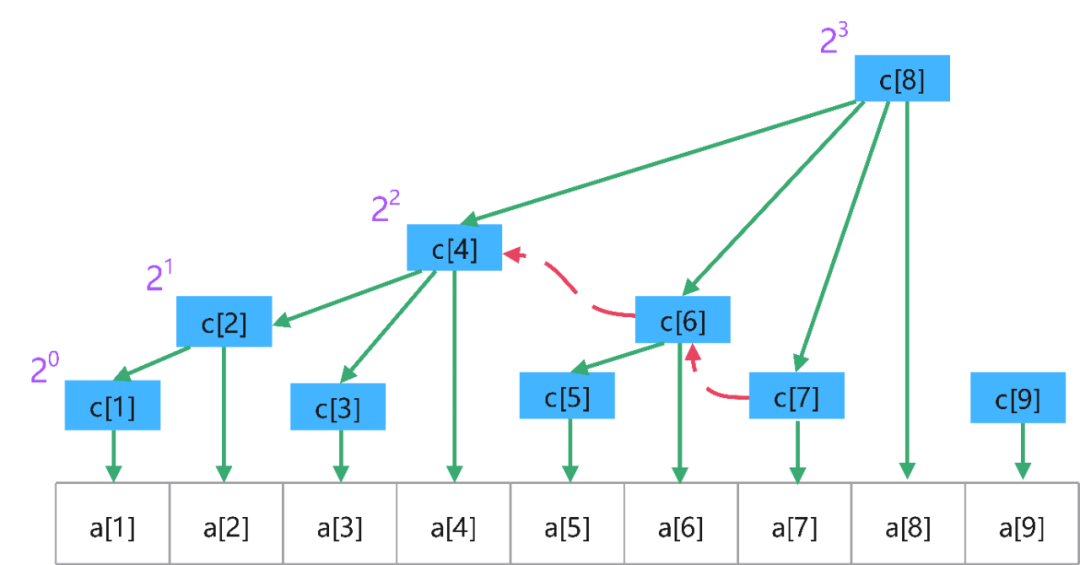
树状数组

1.查询（向下操作）：快速求前缀和 —— O(logn)

2.修改（向上操作）：某个数的值 —— O(logn)

楼兰图腾

该题是树状数组的扩展应用？？

• a[] 待处理的数组

• Greater[i] 记录的是原数组a[i]对应位置上的数的左边比他大的数的个数，lower同理

• tr[] 树状数组——维护值域上的出现次数， tr[x] 表示 x 的出现次数

• add(x, c) 在树状数组中更新位置 x 的值，使其增加 c，并更新所有相关父节点。

• sum(x) 查询树状数组的前缀和（add(x, 1)和重点：即统计数值 ≤x 的总出现次数）。

sum(3) 返回数值 <=3 的总出现次数。

样例解释

5
1 5 3 2 4

打印AC代码后的tr[] 和 sum(x) 的值

    for (int i = 1; i <= n; i ++ )
    {
        int y = a[i];
        Greater[i] = sum(n) - sum(y);
        lower[i] = sum(y - 1);
        cout << "tr[] = "; 
        for (int j = 1; j <= n; ++j) cout << tr[j] << " ";
        cout << ", sum " << n << " = " << sum(n) << " , ";
        cout << "sum " << y << " = " << sum(y) << ", sum " 
             << y - 1 << " = " << sum(y - 1) << endl;
        add(y, 1);
    }

    puts("");

    for (int i = 1; i <= n; ++i) 
        cout << "Greater " << i << " = " << Greater[i] 
             << " , " << "lower " << i << " = " 
             << lower[i] << endl;

tr[] = 0 0 0 0 0 , sum 5 = 0 , sum 1 = 0, sum 0 = 0
tr[] = 1 1 0 1 0 , sum 5 = 1 , sum 5 = 1, sum 4 = 1
tr[] = 1 1 0 1 1 , sum 5 = 2 , sum 3 = 1, sum 2 = 1
tr[] = 1 1 1 2 1 , sum 5 = 3 , sum 2 = 1, sum 1 = 1
tr[] = 1 2 1 3 1 , sum 5 = 4 , sum 4 = 3, sum 3 = 3

Greater 1 = 0 , lower 1 = 0
Greater 2 = 0 , lower 2 = 1
Greater 3 = 1 , lower 3 = 1
Greater 4 = 2 , lower 4 = 1
Greater 5 = 1 , lower 5 = 3

sum(5) - sum(2) ==> 小于等于5的个数 - 小于等于2的个数==大于2且小于等于5的个数 = 3 - 1 = 2